Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 39
Encontre uma equação para a cônica que satisfaz as condições dadas
39. Elipse, focos vértices
Passo 1
Nessa questão, nos foi dado o nome da cônica, seus focos e vértices para encontrarmos sua equação.
Bom, sabemos que é uma elipse, e elipses tem equações no formato:
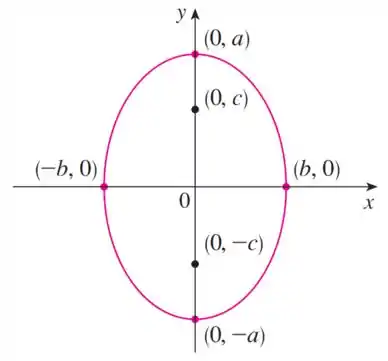
Ou no formato:
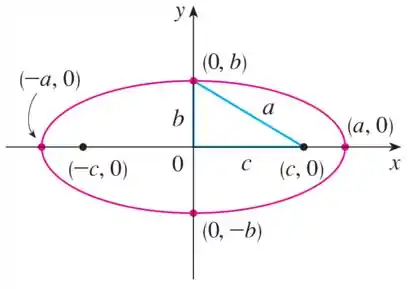
Note que essa é uma elipse com eixo maior no eixo , podemos ver isso pelas coordenadas do vértice, que mudam apenas em .
Por isso nossa equação tem o formato:
Onde é o centro da elipse.
Passo 2
O centro da elipse fica na metade do caminho entre seus vértices, como aqui temos
nosso centro será . Portanto
é a distância do centro da elipse at�� um dos vértices, nesse caso temos
Podemos chamar de a distância do centro da elipse ao foco, então teremos
Também sabemos que existe uma relação entre , tal que , então trocando os valores, encontramos:
Com isso tudo, podemos montar nossa equação:
Colocando as coordenadas do vértice: