Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 34
Encontre uma equação para a cônica que satisfaz as condições dadas
34. Parábola, foco , vértice
Passo 1
Eaee, belezinha??? Bom... Nessa questão, nos foi dado o nome da cônica, seu foco e vértice para encontrarmos sua equação:
Parábola, foco , vértice
Bom, sabemos que é uma parábola, e parábolas tem equações no formato
ou
Mas qual das duas??? A gente pode responder isso analisando os pontos do foco e do vértice que nos foram dados.
Se ambos estiverem alinhados no eixo , então a parábola terá concavidade voltada para esquerda ou direita. Caso for no eixo , terá concavidade para cima ou para baixo.
Com isso, deveremos analisar o deslocamento do vértice em relação a origem para calcularmos , que é um parâmetro que mostra a diferença entre as coordenadas do foco e do vértice.
Assim, descobrimos as variáveis necessárias para a nossa equação!! 😉
Passo 2
Como temos foco e vértice com a primeira coordenada igual, sabemos que essa é uma parábola no eixo , portanto da forma:
O vértice é diferente de , temos um deslocamento em ambos os eixos.
Sabemos que é a diferença entre as coordenadas do foco e do vértice da parábola, portanto:
Juntando tudo isso, podemos montar nossa equação:
Veja a plotagem da nossa parábola:
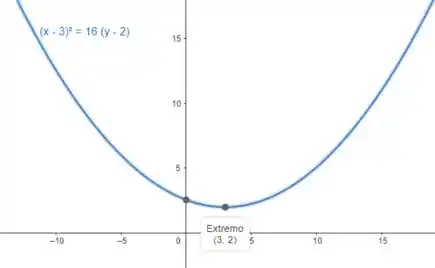
Perceba que o foco e o vértice estão de acordo com o que calculamos 😉