Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 9.1 - Ex. 6
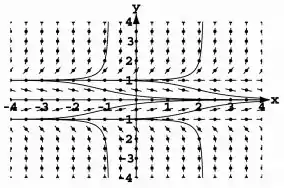
Nos Exercícios 5 e 6, copie os campos de direção e esboce algumas das curvas integrais.
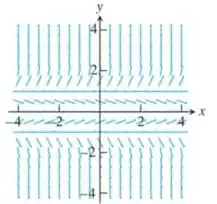
Passo 1
Analisando o desenho do campo de direção, podemos observar que haverá uma reta constante em , e .
Passo 2
Além disso, pode-se pegar intervalos entre esses valores e atribuir pontos que podem ser ligados depois.
Portanto, é possível atribuir valores para em , , e .
Passo 3
Logo, atribuindo valores nesses intervalos e ligando os pontos, pode-se fazer o esboço das curvas seguindo as curvas de direção:
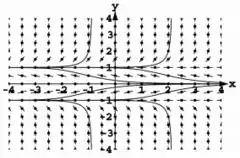
Resposta
Exercícios de Livros Relacionados
Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial dada. Obtenha uma impressão e esboce uma curva solução que passe por ( 0,1 ) . Use o SCA para desen
Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial y ' = y 3 - 4 y . Obtenha uma impressão e esboce as soluções que satisfazem a condição inicial y (
(a) Programe seu sistema de computação algébrica usando o método de Euler com o passo 0,01 para calcular y 2 , onde y é a solução do problema de valor inicial y ' = x 3 - y 3 y 0 = 1 (b) Verifique seu
(a) Programe uma calculadora ou um computador para usar o método de Euler para calcular y 1 , onde y x é a solução do problema de valor inicial d y d x + 3 x 2 y = 6 x 2 y 0 = 3 (i) h = 1 (ii) h = 0,1
Ache a solução completa da equação diferencial (2) d y d t = 6 - 3 x ² ².