(a) Programe seu sistema de computação algébrica usando o método de Euler com o passo para calcular , onde é a solução do problema de valor inicial
(b) Verifique seu trabalho usando o SCA para desenhar a curva solução.
Passo 1
(a) Pessoal, se usarmos o método de Euler num SCA para resolver o problema de valor inicial, com , obteremos:
Passo 2
(b) Vamos desenhar a curva solução:
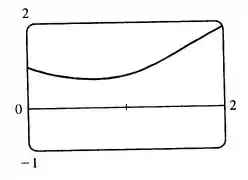
Realmente, olhando para o gráfico, temos .
Resposta
(a)