Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.6 - Ex. 24
Os Exercícios 17-24 nos dão equações para elipses. Coloque cada uma das equações na forma padrão. Em seguida, esboce a elipse. Inclua os focos em seu esboço.
Passo 1
Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Primeiro, temos a equação:
Que devemos colocar na forma padrão. Pela forma padrão de uma equação de elipse, temos que ela tem que ser no formato:
A melhor estratégia é simplificar com base na constante do outro lado da igualdade. Pra nossa questão, simplificando por 4225:
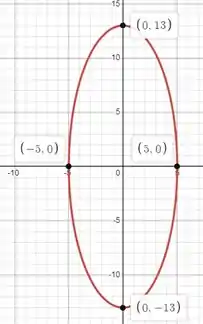
Show, com a equação em mãos, agora é hora de esboçar!
Passo 2
Para o esboço, consideramos o nosso e como os respectivos focos dos eixos e . Para a equação que estamos trabalhando:
Portanto, nossa elipse tem formato:
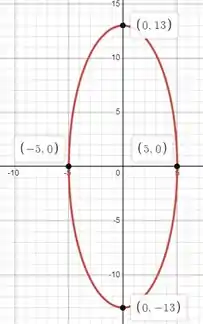
E é isso queridos, até a próxima!
Resposta
