Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.6 - Ex. 43

A hipérbole (x2/16) - (y2/9) = 1 é deslocada 2 unidades para a direita para gerar a hipérbole:

a. Encontre o centro, focos, vértices e assíntotas da nova hipérbole.

b. Represente graficamente os novos centro, focos, vértices e assíntotas e esboce na nova hipérbole.

Passo 1

Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Através da nova equação da cônica após o deslocamento dado por:

Conseguimos determinar então que o entro da antiga cônica é ). Além disso:

Portanto os vértices dela são:

E para a assíntota:

Ou,

Dessa forma:

Logo os focos são:

Passo 2

Após o deslocamento, o novo centro passa a ser:

E os novos vértices e focos após o deslocamento:

E as novas assíntotas:

Esboçando a nova cônica:

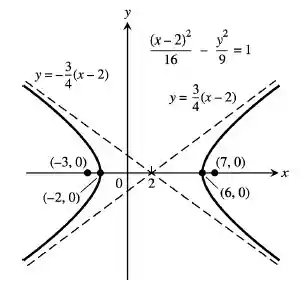
E é isso galera, até a próxima!

Resposta

E as novas assíntotas:

Exercícios de Livros Relacionados

Associe cada uma das seções cônicas nos Exercícios 5-8 com estas equações: x 2 4 + y 2 9 = 1 , x 2 2 + y 2 = 1 y 2 4 - x 2 = 1 , x 2 4 - y 2 9 = 1 Em seguida, encontre os focos e vértices da seção côn

Os Exercícios 17-24 nos dão equações para elipses. Coloque cada uma das equações na forma padrão. Em seguida, esboce a elipse. Inclua os focos em seu esboço. 2 x 2 + y 2 = 4

Os Exercícios 17-24 nos dão equações para elipses. Coloque cada uma das equações na forma padrão. Em seguida, esboce a elipse. Inclua os focos em seu esboço. 169 x 2 + 25 y 2 = 4225

Nos Exercícios 1-8, encontre a excentricidade da elipse. Em seguida, encontre e desenhe os focos e diretrizes da elipse. 16 x 2 + 25 y 2 = 400

Nos Exercícios 1-8, encontre a excentricidade da elipse. Em seguida, encontre e desenhe os focos e diretrizes da elipse. 7 x 2 + 16 y 2 = 112