Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 2.5 - Ex. 15d
Nos exercícios de 2 a 15: d)Esboce seu gráfico.
15-Escreva a equação da superfície de tais que a distâncias de ao ponto é a mesma do que a de ao plano . Identifique a superfície.
Passo 1
d) Galera, no item nós encontramos a seguinte equação para nossa superfície:
Daí nós determinamos seus traços e no item chegamos as seguintes curvas de nível que compõem o gráfico da nossa superfície:
No plano : Parábolas
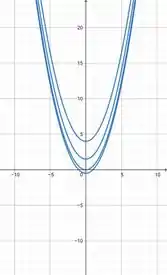
No plano Circunferências
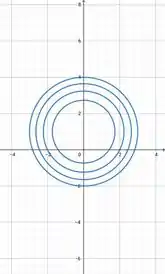
No plano Parábolas
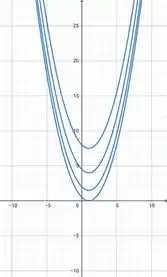
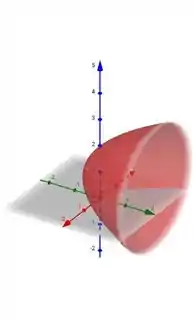
Juntando todas as informações obtidas nos itens anteriores concluímos que se trata de um parabolóide circular. Assim, temos o seguinte gráfico:
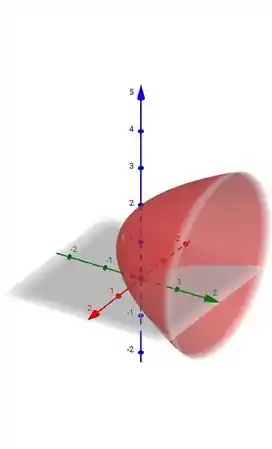
Resposta
Exercícios de Livros Relacionados
Esboce seu gráfico: x 2 + y 2 + z 2 - 2 y - 2 x + 1 = 0
Identifique a superfície: x 2 + y 2 - z 2 - 4 y = 0
Determine os traços: 4 x 2 - 9 y 2 - z 2 = 36
Determine as seções: 4 x 2 - 9 y 2 - z 2 = 36
Identifique a superfície: x 2 + y 2 + z 2 - 2 y - 2 x + 1 = 0