Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 2.5 - Ex. 15b
Nos exercícios de 2 a 15: b)Determine as seções.
15-Escreva a equação da superfície de tais que a distâncias de ao ponto é a mesma do que a de ao plano . Identifique a superfície.
Passo 1
b)Galera, para determinarmos as seções, vamos ter que variar ou , dependendo do plano que estivermos. Isso nos dará as curvas de nível. Fechou ?!
Temos a seguinte superfície:
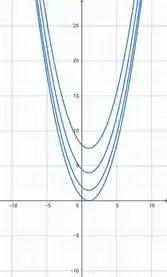
No plano :
Vamos variar o :
Temos uma parábola. Vamos variar o pra ver como vão ficar nossas curvas de nível, para isso vamos construir uma tabela:
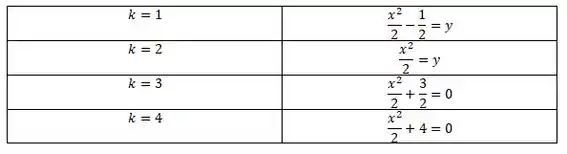
Assim,
Passo 2
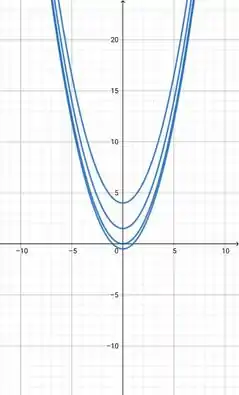
No plano
Vamos variar o :
Temos uma circunferência, na qual o raio varia. Vamos variar o pra ver como vão ficar nossas curvas de nível, para isso vamos construir uma tabela:
Assim,
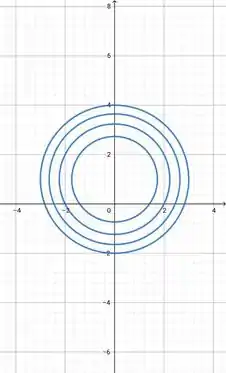
Passo 3
No plano :
Vamos variar o :
Temos uma parábola. Vamos variar o pra ver como vão ficar nossas curvas de nível, para isso vamos construir uma tabela:
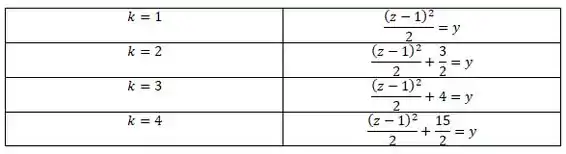
Assim,
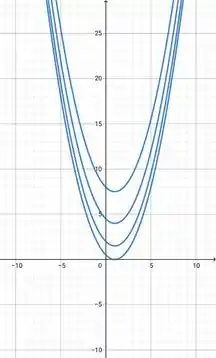
Resposta
No plano :
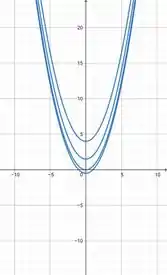
No plano
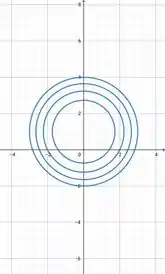
No plano
