Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.4 - Ex. 4
Nos exercícios 1 a 4, para a equação dada,
- Encontre uma equação do gráfico em relação aos eixos , obtidos por uma rotação de um ângulo cuja medida é e
- Faça um esboço do gráfico e mostre os dois conjuntos de eixos.
4)
Passo 1
Primeiramente, precisamos nos lembrar do Teorema 10.4.1 para resolver essa questão de rotação:
Teorema 10.4.1
Se (x,y) for a representação de um ponto P em relação a um conjunto de eixos e for a representação de P após a rotação dos eixos de um ângulo , então
- e
- e
Com no Teorema 10.4.1 (i), obtemos:
e
e
Substituindo essas expressões para x e y na equação , obtemos:
Desenvolvendo os produtos notáveis e simplificando:
Passo 2
A equação obtida no Passo 1 é a equação de uma hipérbole cujas assíntotas são as bissetrizes dos quadrantes no sistema xy. Assim o gráfico da equação é apresentado abaixo:
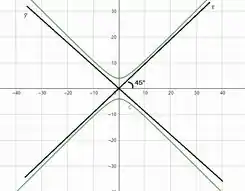
Resposta
a)
b)
Exercícios de Livros Relacionados
Nos exercícios 1 a 4, para a equação dada, Encontre uma equação do gráfico em relação aos eixos x -ey - , obtidos por uma rotação de um ângulo cuja medida é π 4 eFaça um esboço do gráfico e mostre os
Nos exercícios 1 a 4, para a equação dada, Encontre uma equação do gráfico em relação aos eixos x -ey - , obtidos por uma rotação de um ângulo cuja medida é π 4 eFaça um esboço do gráfico e mostre os
Nos exercícios 1 a 4, para a equação dada, Encontre uma equação do gráfico em relação aos eixos x -ey - , obtidos por uma rotação de um ângulo cuja medida é π 4 eFaça um esboço do gráfico e mostre os
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 5 . 24 x y - 7 y 2 + 36 = 0
Nos exercícios de 5 a 12, remova da equação dada o termo x y por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos. 6 . 4 x y + 3 x 2 = 4