Nos exercícios 1 a 7, a equação dada é uma representação implícita de uma superfície S.
- Identifique a superfície
- Escrever algumas representações explícitas de partes de S, representando-as graficamente.
Passo 1
Organizando:
Complementando os quadrados:
Pela equação, temos um elipsoide com centro
Passo 2
Para conseguir representações explícitas, basta isolar os termos:
Isolando x:
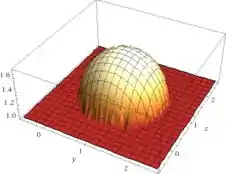
Passo 3
Isolando y:
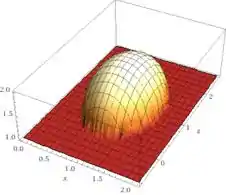
Passo 4
Isolando z:
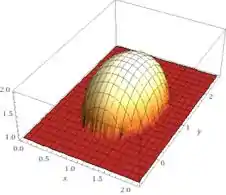
Resposta
elipsoide com centro