Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.3 - Ex. 14
Nos exercícios 8 a 14, obter uma equação cartesiana para a superfície dada. Representá-la graficamente.
Passo 1
Observe a função dada pela questão:
Podemos dizer que a forma geral dessa equação é:
Observando a seção 10.2.3 percebemos que a função acima é semelhando a função paramétrica do cilindro, que é dada por:
e
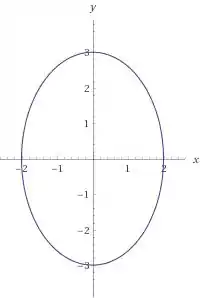
Mas observer que o cilindro da equação dada pela questão possui raios diferentes nas componentes e . Isso nos leva a crer que seja um cilindro de base elíptica.
Sabemos que a formação cartesiana de um cilindro de base circular com raio é:
Então, podemos intuir que para uma base elíptica podemos usar:
Passo 2
Então adaptando a equação: para a forma geral será:
Passo 3
Outra forma de representar a equação paramétrica é utilizando usas componentes:
Passo 4
Aplicando os seguintes limites
Para a equação de
Então os limites da equação são:
Passo 5
Aplicando os seguintes limites
Para a equação de
Então os limites da equação são:
Passo 6
Aplicando os seguintes limites
Para a equação de
Então os limites da equação são:
Passo 7
