Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.3 - Ex. 10
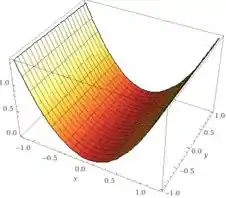
Nos exercícios 8 a 14, obter uma equação cartesiana para a superfície dada. Representá-la graficamente.
Passo 1
Para resolver, vamos utilizar o método da seção 10.2.9. Vamos substituir os elementos livres e por e :
Logo:
Passo 2
Representação gráfica.
No plano XY geramos uma parábola. Como a variação de Z não intefere na parábola, então vamos alogar a parábola infinitamente ao longo de Z.
Resposta
Exercícios de Livros Relacionados
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada.42) Parte do paraboloide z = x 2 + y 2 - 1 , que está estre os planos z = 0 e z = 3 .
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada.45) Parte do plano y + z = 8 , delimitado pelo cilindro x 2 + y 2 = 4 .
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada.44) Parte do plano 2 x + 3 y = 9 , delimitado pelos planos coordenados x = 0 e y = 0 .
Nos exercícios 1 a 7, a equação dada é uma representação implícita de uma superfície S.Identificar a superfície.Escrever algumas representações explícitas de partes de S, representando graficamente. 2
Nos exercícios 1 a 7, a equação dada é uma representação implícita de uma superfície S.Identificar a superfície.Escrever algumas representações explícitas de partes de S, representando graficamente. 2