Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.5 - Ex. 1
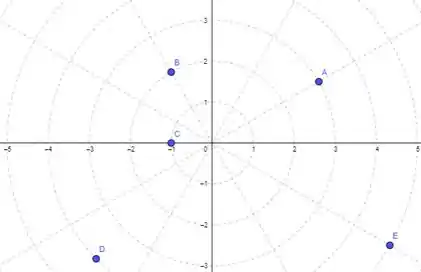
Nos exercícios de 1 a 4, marque o ponto com o conjunto de coordenadas polares dadas.
1.
Passo 1
Neste tipo de questão na hora de marcar os pontos em coordenadas polares devemos primeiro marcar o ângulo tendo seu vértice na origem do eixo polar e seu lado inicial ao longo do eixo polar. Após isso, marcamos o valor do seu raio.
Passo 2
Sendo assim, o os pontos envolvidos nesta questão podem ser representados por:
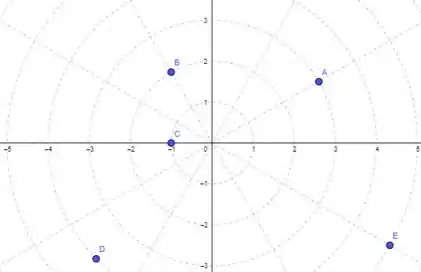
Resposta
Exercícios de Livros Relacionados
Prove que os gráficos de r= a θ e r θ = a têm um numero ilimitado de pontos de intersecção. Pronve também que as retas tangentes a esses pontos são perpendiculares.
Para a curva r = 2 ( 1 + s e n θ ) , ache X e α no ponto (1, 2 3 π ) . Faça um esboço da curva mostrando X e α .
Para a curva r = 2 cos 1 2 θ ache X e α no ponto (1, 1 6 π ) . Faça um esboço da curva mostrando X e α .
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com