Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.4 - Ex. 4
Nos Exercícios 1-6, dê as posições de um corpo que se desloca em um eixo, sendo dado em metros e em segundos.
- Determine o deslocamento do corpo e a velocidade média para o intervalo dado.
- Determine o módulo de velocidade e a aceleração do corpo nas extremidades do intervalo.
- Quando, se de fato acontece, o corpo muda de direção durante o intervalo?
Passo 1
Na letra a.) o exercício pede para determinamos o deslocamento do corpo e a velocidade méida. Para determinar o deslocamento precisamos calcular o que é igual a:
Como o intervalo foi de ,
Já a velocidade média é calculada a partir do deslocamento do corpo pela tempo decorrido:
Passo 2
Na letra b.) é pedido o módulo de velocidade e a aceleração do corpo nas extremidades do intervalo. Como a velocidade é a variação do espaço pelo tempo, velocidade é a derivada de ordem 1 da função .
Como ele quer o módulo nas extremidades do intervalo:
A aceleração é a variação da velocidade pelo tempo decorrido, então a aceleração é a segunda derivada da função :
Como o exercício pede a aceleração nas extremidades do intervalo:
Passo 3
Para resolvermos a letra c.) precisamos lembrar que um corpo muda de direção quando a sua velocidade fica nula. Logo,
Utilizando Bhaskara:
Para facilitar foi feito um esboço do gráfico de velocidade.
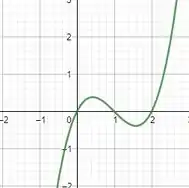
Observando o gráfico de , é possível observar que muda de direção nas três raízes, porém em a mudança acontece fora do intervalo estipulado, por isso há mudança de direção em e .