Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.15 - Ex. 19

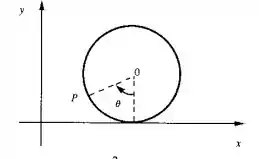
O ponto P = x ,   y está fixo à roda de raio 1 m, que rola, sem escorregamento, sobre o eixo x . O ângulo θ está variando a uma taxa constante de 1 rad/s. Expresse as velocidades da abscissa e da ordenada de P em função de θ .

Passo 1

Oi, galerinha! Tudo bom? O lance mais importante aqui é sacar que essa roda além de girar também anda para direita!

Vamos olhar primeira para rotação! Por trigonometria, temos que o valor do eixo x será dado por uma relação com o cosseno e o de y com o seno. Assim:

x = r cos ⁡ θ

y = r sen ⁡ θ

Como o raio da roda é 1

x = cos ⁡ θ

y = sen ⁡ θ

Agora vamos olhar para o movimento dela andando pelo eixo x . Pra isso a gente tem que pensar o seguinte: para um certo movimento angular θ a esfera andará uma distância r θ . Como o raio é 1 essa distância é θ .

Como no eixo ela anda e roda, vamos fazer um somatório dos dois movimentos. Assim as coordenadas passam a ser

x = cos ⁡ θ + θ

y = sen ⁡ θ

Agora que entendemos o movimento, vamos derivar!

Passo 2

Assim, derivando ambas as relações em relação a t , temos:

Para y temos,

y = sen ⁡ θ

d y d t = cos ⁡ θ ⋅ d θ d t

Para x temos,

x = cos ⁡ θ + θ

d x d t = - sen ⁡ θ ⋅ d θ d t + d θ d t

Passo 3

Nos foi dado que ângulo θ está variando a uma taxa constante de 1 rad/s, ou seja, d θ d t = 1 . Então:

d y d t = cos ⁡ θ

E

d x d t = - sen ⁡ θ + 1

Logo,essas são as velocidades da abscissa e da ordenada de P em função de θ .

Resposta

d x d t = - sen ⁡ θ + 1 e d y d t = cos ⁡ θ .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Se $ 1000 forem emprestados a 8 % de juros, encontre as quantias devidas ao fim de três anos se os juros forem compostos ( i ) anualmente, ( i i ) trimestralmente, ( i i i ) mensalmente, ( i v ) s
Se y = x ³ + 2 x ³ e d x d t = 5 , encontre d y d t quando x = 2 .
1) Se V for o volume de um cubo com aresta de comprimento x e, à mediada que o tempo passa, o cubo se expandir, encontre d V d t em termos de d x d t .
O raio de uma esfera está aumentando a uma taxa de 4 mm/s. Quão rápido o volume estará aumentando quando o diâmetro for 80 mm?
Se z 2 = x 2 + y 2 , d x d t = 2 e d y d t = 3 , encontre d z d t quando x = 5 e y = 12 .