Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.2 - Ex. 4
Nos exercícios de 1 a 7 representar graficamente os seguintes campos vetoriais.
4)
Passo 1
Bom galera, aqui não é nada muito complicado, mas é um pouco diferente, já que o vetor tem um tamanho e uma direção definida, independente dos valores de (x, y).
Então nosso desenho será assim:
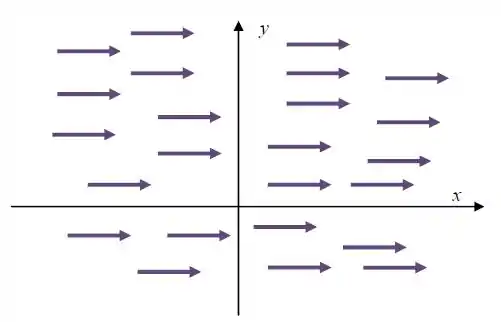
Tranquilinha?
Resposta
Exercícios de Livros Relacionados
10. Encontre o ponto na curva unidades ao longo da curva a partir do ponto (0, -12, 0) na direção do comprimento de arco crescente.
Resolva os problemas de valor inicial nos Exercícios 11-16 para r como uma função vetorial de t.Equação diferencial: d 2 r d t 2 = - 32 k Condição inicial: r 0 = 100 k e d r d t t = 0 = 8 i + 8 j
Comprimento é independente da parametrização Para ilustrar que o comprimento de uma curva espacial suave não depende da parametrização utilizada para computá-lo, calcule o comprimento de uma volta da
Nos Exercícios 11-14, encontre o parâmetro de comprimento de arco ao longo da curva a partir do ponto em que t = 0, avaliando a integral s = ∫ 0 t v τ d τ da Equação 3. Em seguida, encontre o comprime
Distância ao longo de uma reta Mostre que, se u é um vetor unitário, então o parâmetro de comprimento de arco ao longo da reta r(t) = P 0 + tu a partir do ponto P 0 ( x 0 ,y 0 ,z 0 ) , em que t = 0, é