Explique a diferença entre um máximo relativo e um absoluto. Esboce um gráfico que exiba uma função com um máximo relativo que não é absoluto e exiba um outro gráfico

com um máximo absoluto que não é relativo. Explique como esses gráficos satisfazem as condições dadas.

Bom, vamos lá! Um máximo absoluto é um ponto com maior valor do gráfico de uma

função. Já o máximo relativo é o ponto onde um pico com valor alto é encontrado, porém não temos certeza se é o maior valor.

Para expressar um gráfico que exiba uma função com um máximo absoluto que não é relativo, temos a função , entre o intervalo . Assim, temos:

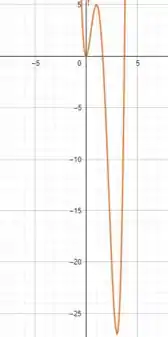
Portanto, vemos que é um máximo local, enquanto o máximo absoluto é . Este máximo absoluto não é um máximo local, pois ele ocorre em extremo do intervalo.

E, por fim, para um gráfico que exiba uma função com um máximo relativo que não é absoluto:

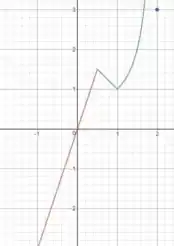
Em temos uma máximo local, porém, quando estamos em onde ela é definida no intervalo todo.

Prontinho!!