Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.1 - Ex. 39

Dizemos que duas curvas são ortogonais se suas retas tangentes forem perpendiculares em cada ponto de intersecção, e dizemos que duas famílias de curvas são trajetórias ortogonais uma da outra se cada membro de uma família for ortogonal a cada membro da outra. Essa terminologia é usada nestes exercícios.

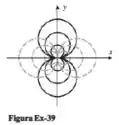
A Figura Ex-39 mostra alguns membros típicos das famílias dos círculos x 2 + y – c 2 = c 2 (curvas escuras) e x - k 2 + y 2 = k 2 (curvas cinzas). Mostre que essas famílias são trajetórias ortogonais uma da outra. [Sugestão: Para as retas tangentes serem perpendiculares

em um ponto de intersecção, as inclinações dessas retas tangentes devem ser recíprocas negativas uma da outra.]

Passo 1

Primeiro, vamos derivar implicitamente a função x - k 2 + y 2 = k 2 . Tratamos y como uma função y ( x ) e derivamos ambos os lados:

d d x x - k 2 + y 2 = d d x k 2

2 x - k + 2 y d d x y = 0

2 x - k + 2 y y ' = 0

Passo 2

Após a derivação, isolamos k :

2 x - 2 k + 2 y y ' = 0   : 2

x - k + y y ' = 0

k = x + y y '

Substituindo na expressão inicial:

x - ( x + y y ' ) 2 + y 2 = ( x + y y ' ) 2

Isolamos, agora, o y :

x - x + y y ' 2 + y 2 = x + y y ' 2

y y ' 2 + y 2 = x 2 + 2 x y y ' + y y ' 2

y 2 = x 2 + 2 x y y '

y ' = y 2 - x 2 + 1 2 x y

Para obtermos a família ortogonal às curvas cinzas, invertemos a expressão e resolvemos a EDO.

- 1 y ' = y 2 - x 2 + 1 2 x y         ∴         y ' = 2 x y y 2 - x 2 + 1

Assim, obteremos a solução:

x 2 + y – k 2 = k 2

Prontinho!!

Resposta

A demonstração confere!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18. Calcular y ' = d y d x das sequintes funções definidas implicitamentea) x 3 + y 3 = a 3 b) x 3 + x 2 y + y 2 = 0 c) x + y = a d) y 3 = x - y x + y e) a cos 2 ⁡ ( x + y ) = b f) tg ⁡ y = x y e) e y
18. Calcular y ' = d y d x das sequintes funções definidas implicitamentea) x 3 + y 3 = a 3 b) x 3 + x 2 y + y 2 = 0 c) x + y = a d) y 3 = x - y x + y e) a cos 2 ⁡ ( x + y ) = b f) tg ⁡ y = x y g) e y
18. Calcular y ' = d y d x das sequintes funções definidas implicitamentea) x 3 + y 3 = a 3 b) x 3 + x 2 y + y 2 = 0 c) x + y = a d) y 3 = x - y x + y e) a cos 2 ⁡ ( x + y ) = b f) tg ⁡ y = x y e) e y
18. Calcular y ' = d y d x das sequintes funções definidas implicitamentea) x 3 + y 3 = a 3 b) x 3 + x 2 y + y 2 = 0 c) x + y = a d) y 3 = x - y x + y e) a cos 2 ⁡ ( x + y ) = b f) tg ⁡ y = x y e) e y
18. Calcular y ' = d y d x das sequintes funções definidas implicitamentea) x 3 + y 3 = a 3 b) x 3 + x 2 y + y 2 = 0 c) x + y = a d) y 3 = x - y x + y e) a cos 2 ⁡ ( x + y ) = b f) tg ⁡ y = x y g) e y