Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.5 - Ex. 20

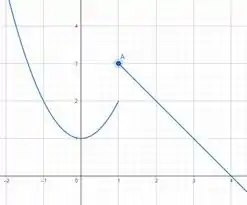
Explique por que a função é descontínua no número dado, esboce o gráfico da função.

f x = 1 + x 2 ,         s e   x < 1 4 - x ,       s e   x ≥ 1                                                       a = 1

Passo 1

Opa, bora lá! O enunciado nos dá a função:

f x = 1 + x 2 ,         s e   x < 1 4 - x ,       s e   x ≥ 1                                                      

E pede pra a gente explicar por que ela é descontínua em x = 1 . Para verificar se a função é contínua ou não, duas condições devem ser satisfeitas:

- o limite deve existir naquele ponto, ou seja, os limites laterais, naquele ponto, devem ser iguais:

lim x → 1 - ⁡ f x = lim x → 1 + ⁡ f x

- o limite naquele ponto deve ter o mesmo valor que a função:

lim x → 1 ⁡ f x = f x

Depois vamos esboçar o gráfico da função. Repara que temos uma função definida por partes. Isso quer dizer que em cada parte que é diferente o gráfico vai ter uma carinha diferente.

Passo 2

Sendo assim, vamos calcular os limites laterais fazendo

lim x → 1 - ⁡ f x = l i m x → 1 -   1 + x 2

= 1 + 1 2

= 2

l i m x → 1 + f x = l i m x → 1 + 4 - x

= 4 - 1

= 3

Como o limite bilateral não existe, nossa função já não atende ao critério de continuidade do limite existir para esse ponto.

Passo 3

Para esboçar o gráfico, repara que para valores de x < 1 a carinha da função vai ser f x = 1 + x 2 e para valores de x ≥ a carinha vai ser f x = 4 - x :

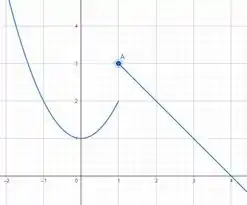
Prontinho!

Resposta

  1. Demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Explique por que cada função é contínua os descontínua.a) A temperatura em um local específico como função do tempo.b) A temperatura em um tempo específico como função da distância em direção a oeste
Encontre os pontos nos quais f é descontínua. Em quais desses pontos f é contínua à direita, à esquerda ou em nenhum deles? Esboce o gráfico de f . f x = x + 2 e x2 - x s ex0 s e0 ≤ x ≤ 1 s ex1
A força gravitacional exercida pela Terra sobre uma unidade de massa a uma distância r do centro do planeta é F r = G M r R 3s erR G M r 2 s er ≥ R Onde M é a massa da Terra; R é seu raio; e G é a con
Para quais valores da constante c a função f é contínua em - ∞ , ∞ ? f x = c x 2 + 2 x ,s ex2 x 3 - c x ,s ex ≥ 2
Encontre os valores de a e b que tornam a função f contínua em toda a parte. f x = x 2 - 4 x - 2 s ex2 a x 2 - b x + 3s e2x3 2 x - a + b s ex ≥ 3 .