Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.8 - Ex. 1
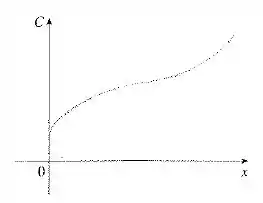
Um fabricante mantém registros precisos do custo da produção de itens e obtém um gráfico da função custo mostrado na figura.
- Explique por que .
- Qual a significância do ponto de inflexão?
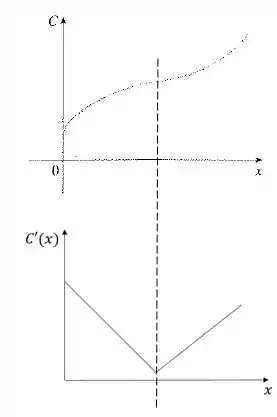
- Use o gráfico de para esboçar o gráfico da função custo marginal.
Passo 1
- O valor representa o custo dado pela produção de nenhum item. Esse valor é maior que zero pois há custos fixos envolvidos no processo, como por exemplo pagamentos da estrutura da fábrica (luz, aluguel, etc), que deverão ser feitos mesmo que não se produza nada.
- O ponto de inflexão de uma função ocorre quando a derivada dela para de decrescer e começa a crescer ou o contrário. Nesse caso, a derivada do custo é o custo marginal, que para de diminuir e passa a crescer depois do ponto de inflexão (a inclinação da reta está diminuindo depois começa a crescer). Isso acontece por que em dado momento, quando se produzem poucos itens, aumentar o número de itens faz com que o custo fixo seja mais bem aproveitado, pois o custo fixo por produto diminui. Por exemplo, se tivermos 10 mil reais como custo fixo, ao passarmos de 10 para 20 itens o custo fixo por item diminui de 1000 para 500. Isso faz com que o custo marginal empregado na produção de mais um item seja menor. Mas a partir de certo ponto, ocorrem fatores que fazem com que a fabricação de mais itens não seja mais vantajosa, por ter que pagar horas extras ou problemas de funcionamento de máquinas por produção de muitas unidades. Assim começa a aumentar de novo.
- Podemos ver que a inclinação da reta tangente começa positiva, vai decrescendo até um valor próximo de zero (curva quase horizontal) e então volta a subir. Um esboço da curva de seria então o seguinte:
Passo 2
Passo 3
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
17. Uma bola de bilhar é atingida e movimenta-se em linha reta. Se s cm for a distância da bola de sua posição inicial após t s, então s = 100 t 2 + 100 t . Com qual velocidade a bola atingirá a tabel
3. Uma partícula move-se ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância orientada da partícula a partir do ponto O em t s. Ache a velocidade instantânea v ( t )
5. Uma partícula move-se ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância orientada da partícula a partir do ponto O em t s. Ache a velocidade instantânea v ( t )
Nos exercícios de 39 a 42, uma partícula move-se ao longo de uma reta de acordo com a equação dada, onde s cm é a distância orientada da partícula até a origem, em t s. (a) Qual será a velocidade da p
A força eletromotriz de um circuito elétrico com um gerador simplificado é E ( t ) volts em t s, onde E t = 50 s e n 120 π t . Ache a taxa de variação instantânea de E ( t ) em relação a t em (a) 0,02