Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.1 - Ex. 11

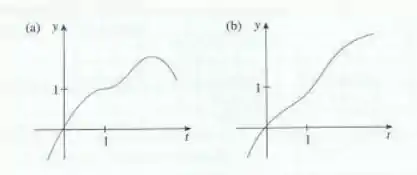
Explique porque as funções cujos gráficos são dados a seguir não podem ser soluções da equação diferencial d y d t =   e t y - 1 2

Passo 1

Nessa questão nós precisamos analisar a equação diferencial d y d t =   e t y - 1 2 e descobrir porque os gráficos dados não podem ser solução para ela.

Bom, podemos dividir a equação em duas partes para fazer essa análise, vamos olhar separadamente para e t e para y - 1 2

Passo 2

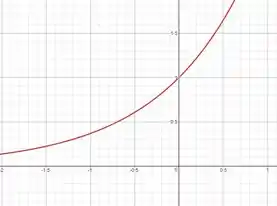
Note que e t é uma função exponencial e por isso é sempre positiva, também podemos ver isso pelo gráfico:

Passo 3

Agora vamos olhar para y - 1 2 . Note que y - 1 2 ≥ 0 , para qualquer número y real, pois está elevado ao quadrado. Podemos tirar essa conclusão também pelo gráfico da função:

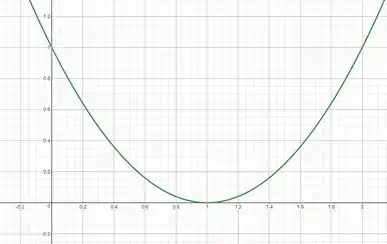
Como e t e y - 1 2 são positivos, então d y d t =   e t y - 1 2 ≥ 0

Passo 4

  1. Então o gráfico do item (a) não pode ser solução para a EDO pois ele é decrescente a partir de um ponto

    2. Passo 5

  2. Quando y = 1 , d y d t =   e t y - 1 2 = 0

Precisamos lembrar então que qundo a derivada de uma função é igual a 0 , nós temos uma reta tangenet horizontal nesse ponto. Observe que no gráfico do item (b) isso não acontece. Portanto essa não pode ser a solução da EDO.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a solução completa da equação diferencial (1) d y d t = 4 x - 5 .
Ache a solução completa da equação diferencial (8) d y d x = x ² ( x 3 - 3 ) y ² ² ².
Ache a solução completa da equação diferencial (3) d y d t = 3 x 2 + 2 x - 7 .
Ache a solução completa da equação diferencial (4) d s d t = 5 s .
Ache a solução completa da equação diferencial (13) d ² s d t ² = s e n 3 t + c o s 3 t ² ² .