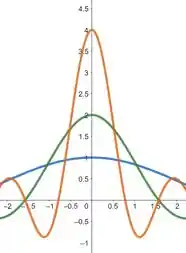
Explorando : Esboce em um único gráfico , e no intervalo . Onde cada gráfico parece cruzar o eixo ? Os gráficos realmente cortam os eixos? O que você espera dos gráficos e quando ? Por quê? E do gráfico de para outros valores de ? Justifique suas respostas.

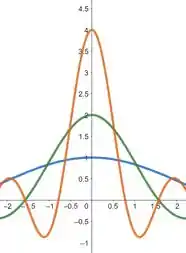
Vamos começar por esboçar os gráficos das funções , e no intervalo . Sendo assim, temos:

Os gráficos das funções aparentam cruzar o eixo nos seguintes valores:

• cruza em ;
• cruza em
• cruza em

Os gráficos das funções analisadas anteriormente realmente não cruzam o eixo . Isto ocorre pois o ponto não pertence ao domínio das funções. Como elas são funções racionais, o denominador dela não pode ser igual a . É por isto que o domínio das três funções é:

Os gráficos das funções e tendem aos valores e quando , respectivamente. Isto decorre do limite que discutido no próximo passo.

Para melhor explicar o passo anterior e o que acontece com funções do tipo quando , vamos resolver o limite dessas funções. Assim temos:

Se fizermos uma mudança de variável, chamar , quando , . Desta forma, temos:

Desta forma, chegamos a um dos limites fundamentais do seno. Como:

Temos:

Desta forma, fica claro o que ocorre quando para as funções descritas nesta questão.