Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.8 - Ex. 35
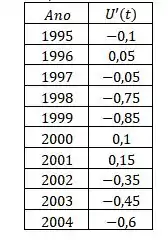
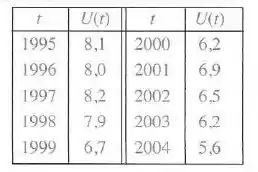
A taxa de desemprego varia com o tempo. A tabela fornece a porcentagem de desempregados na força de trabalho australiana em meados de 1995 a 2004.
- Qual o significado de ? Quais são as suas unidades?
- Construa a tabela de valores de .
Passo 1
E aí, galerinha! 😉
Nesse problema foi dada uma tabelinha com alguns valores e nosso objetivo é dizer qual o significado de e constuir uma tabela com os valores de .
Parece complicado? 🤔
Para obter as derivadas de valores discretos como nesse caso, podemos simplificar a definição de derivada
Bora começar! 😉
Passo 2
Primeiramente, é a taxa na qual a taxa de desemprego está mudando em relação ao tempo. Suas unidades são porcentagem por ano.
Bacana, não é? 😊
Passo 3
Podemos encontrar o valor da derivada fazendo
Como vimos no passo 1.
- Então, para 1995, fazemos
- Agora, para 1996 devemos calcular tanto a variação para frente quanto para trás e tirar a média destes valores
- Para 1997
- Para 1998
Obs: Note que , ou seja, a variação de um ano em relação ao seu anterior, é igual a variação do ano anterior com o ano atual, logo, não calcularemos duas vezes a partir daqui.
Tranquilo até aqui? 😇
Passo 4
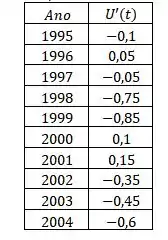
Repetindo o processo até o ultimo valor podemos construir a tabela
E aí! entendeu tudo? Responde Aí! 😎
Resposta
- é a taxa na qual a taxa de desemprego está mudando em relação ao tempo. Suas unidades são porcentagem por ano
