Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 39
Expresse a quantidade dada como um único logaritmo.
37)
Passo 1
Opa, bora lá! Temos:
E temos que escrever esse carinha na forma de:
Pra resolver isso temos que ter em mente as propriedades de :
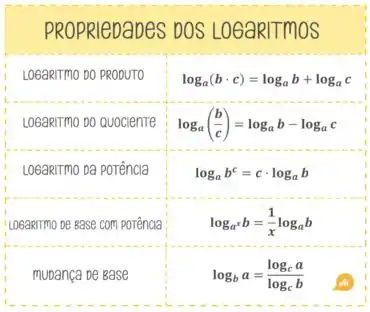
A ideia é ir usando essas propriedades pra simplificar o máximo possível a nossa expressão!
Passo 2
Aqui a gente tem:
Usando a propriedade de logaritmo da potência, podemos dizer que:
Até aqui tranquilo, né?
Passo 3
Aqui a gente tem dois logaritmos na mesma base, que no caso é a base natural . Então podemos usar o logaritmo do produto:
Então:
Multiplicando, temos:
Então:
Prontinhoo!
Resposta
Exercícios de Livros Relacionados
55. De acordo com uma fonte, o barulho dentro de um carro em movimento está em torno de 70 dB, enquanto um liquidificador gera 93 dB. Encontre a razão da intensidade do barulho do liquidificardor com
51. A acidez de uma substãncia é medida pelo valor de se p H , o qual é definido pela fórmula p H = - log H + Onde o símbolo H + denota a concentração de ions de hidrogênio, medida em moles por litr
54. Se um som for três vezes tão intenso quanto o outro, quanto maior será seu nível em decibéis?
57. Na escala Richter, a magnitude M de um terremoto está relacionada com a energia liberada E, em joules(J), pela equação log E = 4,4 + 1,5 M Encontre a energia E do terremoto de San Francisco de 1
52. Use a definição de p H do Exercicio 51 para encontrar a H + da solução que tem um p H igual a:2,448,06