51. A acidez de uma substãncia é medida pelo valor de se , o qual é definido pela fórmula
Onde o símbolo denota a concentração de ions de hidrogênio, medida em moles por litro. A agua destilada tem um igual a 7; uma substancia é considerada ácida se tiver e básica se tiver . Encontre de cada uma das seguintes substãncias e estabeleça se é acida ou básica.
Passo 1
Belezoca de motoca galera, o enunciado deu pra gente a fórmula que calcula o , dada por:
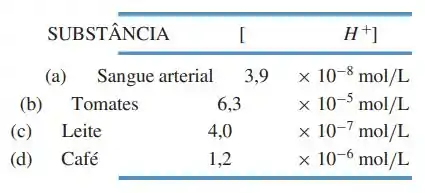
E deu também uma tabela com o valor da concentração de íons de hidrogênio, :
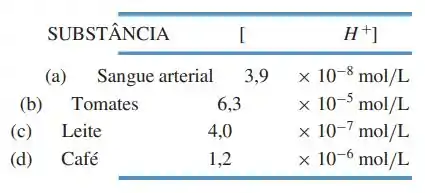
Então para descobrir o valor do , dessas substâncias, é só a gente substituir o valor de na função do . Bora lá então.
Passo 2
Saca só, na letra (a), ele diz que o Sangue arterial possui uma concentração de ions numa escala dada como:
E jogando este valor na fórmula, temos que:
Aplicando a propriedade da soma de logaritmos, chegamos em:
E aplicando também a propriedade dos expoentes dentro do logaritmos, temos que:
Juntando tudo, e levando em consideração que , obtemos:
Logo, ele se encaixa em um básico.
Passo 3
Show de bolas, agora na letra (b), ele diz que os Tomates possuem uma concentração de ions numa escala dada como:
E jogando este valor na fórmula, temos que:
Aplicando a propriedade da soma de logaritmos, chegamos em:
E aplicando também a propriedade dos expoentes dentro do logaritmos, temos que:
Juntando tudo, e levando em consideração que , obtemos:
Logo, ele se encaixa em um , ácido.
Passo 4
Belezinha então meus xuxus, iremos fazer mais ou menos a mesma coisa agora com o Leite, se liga, a concentração dele é:
E jogando este valor na fórmula, temos que:
Aplicando a propriedade da soma de logaritmos, chegamos em:
E aplicando também a propriedade dos expoentes dentro do logaritmos, temos que:
Juntando tudo, e levando em consideração que , obtemos:
Portanto, ele se encaixa em um , ácido.
Passo 5
Iradoso, a mesma coisa acontece com o Café:
E jogando este valor na fórmula, temos que:
Aplicando a propriedade da soma de logaritmos, chegamos em:
E aplicando também a propriedade dos expoentes dentro do logaritmos, temos que:
Juntando tudo, e levando em consideração que , obtemos:
Portanto, ele se encaixa em um , ácido.
Resposta
- , básico.
- , ácido.
- , ácido.
- , ácido.