Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.8 - Ex. 67
Um fabricante de lâmpadas quer produzir lâmpadas que durem cerca de horas, mas naturalmente algumas lâmpadas queimam mais rapidamente que outras. Seja a fração de lâmpadas da companhia que queimam antes de horas; assim está entre e .
Faça um esboço de como você acha que o gráfico de deve parecer.
Qual o significado da derivada ?
Qual o valor de ? Por quê?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos disse que o fabricante quer fazer com que as lâmpadas durem cerca de horas, só que ele tem o problema delas queimarem antes de horas e são definidas pela função , que está entre e .
Ele pediu pra gente esboçar um gráfico estimado de , dizer qual o significado da derivada e calcular o valor de .
Então, vamos lá interpretar esse problema e calcular a integral pedida.
Passo 2
Nós podemos esperar que uma pequena porcentagem de lâmpadas queime nas primeiras centenas de horas, e a maioria das lâmpadas queime depois, perto de horas, com algumas delas queimando continuamente.
Assim, podemos esboçar o gráfico de na forma:
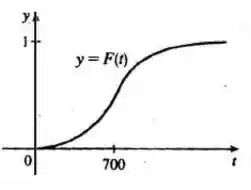
Sendo assim, a derivada é a taxa na qual a fração de lâmpadas da companhia que queimam antes de horas aumenta conforme as horas passam, ou seja, conforme aumenta.
Passo 3
Agora vamos entender o significado da integral:
Observe que ela é a integral da derivada da nossa função . Logo, ela é igual a quando o tempo vai de até infinito, ou seja:
Como o enunciado nos diz que está entre e , temos:
Isso ocorre porque para a variação de tempo especificada da integral , temos que todas as lâmpadas, irão queimar algum dia.
Valeu, galera! Até a próxima! 😉
Resposta
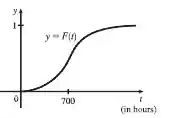
A derivada é a taxa na qual a fração de lâmpadas da companhia que queimam antes de horas aumenta conforme aumenta.
Isso ocorre pois na variação de tempo especificada da integral , temos que todas as lâmpadas, irão queimar algum dia.