Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 51
Encontre o volume do sólido descrito. Uma pirâmide de altura e base retangular de lados e .
Passo 1
Fala aí, galerinha! 😉
Nesse problema queremos obter o volume de uma pirâmide de altura e base retangular de lados e ...
Perce complicado? 😐
Para um corte transversal de altura , nós vemos por semelhança de triângulos que , logo, . Similarmente, para um corte transversal tendo como sua base e substituindo ,
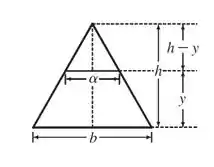
Tranquilo até aqui? 😉
Passo 2
Assim, nosso volume é:
Simplificando...
Calculando a integral, temos
Isso é igual a , onde é a área da base, como em qualquer pirâmide.
E aí! O que achou? Responde Aí! 😬
Resposta
Exercícios de Livros Relacionados
3 - O sólido está situado entre os planos perpendiculares ao eixo x em x = π 4 e x = 5 π 4 As seções transversais entre esses planos são discos circulares cujos diâmetros vão da curva y = 2 cos x à
Nos Exercícios 1-10, determine os volumes dos sólidos.5- A base de um sólido é a região entre a curva y = 2 sen x e o intervalo [ 0 , π ] no eixo x . As seções transversais perpendiculares ao eixo x
Nos Exercícios 1-10, determine os volumes dos sólidos.5- A base de um sólido é a região entre a curva y = 2 sen x e o intervalo [ 0 , π ] no eixo x . As seções transversais perpendiculares ao eixo x
Nos Exercícios 1-10, determine os volumes dos sólidos.8- A base de um sólido é a região limitada pelos gráficos de y = x e y = x / 2 . As seções transversais perpendiculares ao eixo x são: Triângulo i
Nos Exercícios 1-10, determine os volumes dos sólidos.3- O sólido está situado entre planos perpendiculares ao eixo x em x = - 1 e x = 1 . As seções transversais perpendiculares ao eixo x entre esses