Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 3

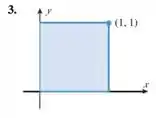
Faça uma conjectura sobre as coordenadas do centroide da região e confirme-a por integração.

Passo 1

A ideia aqui é estimar o centroide dessa placa pensando na simetria dela e depois usar nossa fórmulinha para confirmar:

x - = 1 á r e a   d e   R   ∫ a b x ( f x - g x ) d x

y - = 1 á r e a   d e   R   ∫ a b 1 2 f x 2 - g x 2 d x

Passo 2

Nossa placa é um quadrado. Ele é simétrico tanto vertical quanto horizontalmente. Isso significa que o centroide vai fazer bem no meio.

Como ele tem lado 1 , e o vértice está na origem, é só dividir 1 por 2 .

x - , y - = 1 2 , 1 2

Passo 3

Vamos achar as coordenadas do centroide por integração. Primeiro a coordenada x - :

x - = 1 á r e a   d e   R   ∫ a b x ( f x - g x ) d x

No eixo x nossa região está entre 0 e 1 , e no eixo y , nossa região está entre y = f x = 1 (por cima) e y = g x = 0 (por baixo).

Como é um quadrado de lado 1 , a área é 1 também.

Nossa integral fica:

x - = 1 1   ∫ 0 1 x ( 1 - 0 ) d x = ∫ 0 1 x d x = 1 2

Passo 4

Agora a coordenada y - :

y - = 1 á r e a   d e   R   ∫ a b 1 2 f x 2 - g x 2 d x

y - = 1 1 ∫ 0 1 1 2 1 2 - 0 2 d x = 1 2

Viu? Deu igualzinho!

Resposta

x - , y - = 1 2 , 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nestes exercícios, quando necessário, consulte a Tabela 6.8.2 para os pesos específicos dos fluidos.(a) Encontre a força (em N ) sobre o convés de um navio afundado se sua área for de 160m 2 e a press
As superfícies planas mostradas estão imersas verticalmente em água. Encontre a força do fluido sobre cada superfície.
As superfícies planas mostradas estão imersas verticalmente em água. Encontre a força do fluido sobre cada superfície.
Suponha que uma superfície plana esteja imersa verticalmente em um fluido de peso específico ρ . Dobrando-se ρ , dobra também a força sobre a superfície? Explique seu raciocínio.
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.A pressão e a força têm as mesmas unidades no sistema M K S .