Faça uma conjectura sobre as equações das assíntotas horizontais, se houver, por meio do gráfico da equação obtida por um recurso computacional; verifique sua resposta usando a regra de L’Hôpital.
56.
Passo 1
Temos o seguinte gráfico para a função:
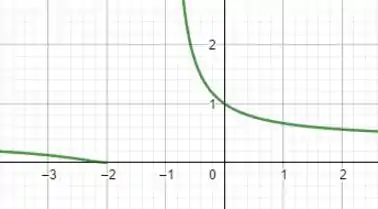
Passo 2
Pra verificarmos a equação da assíntota vertical que vemos que deve existir no gráfico, podemos calcular o limite da função para quando tende a (+) infinito, usando a regra de L’Hôpital.
Vamos ter:
Se aplicamos diretamente na função, teríamos a indeterminação:
Passo 3
Essa indeterminação não nos permite usar diretamente a regra de L’Hôpital, portanto precisamos mexer um pouco na nossa função pra usá-la.
Passo 4
Existe uma propriedade matemática que diz o seguinte:
Reescrever nossa função dessa maneira e calcular o limite vai nos ajudar a chegar em uma indeterminação , passível de se usar a regra de L’Hôpital!
Vamos ter:
Como a função exponencial é contínua, vale a propriedade de que o limite dessa função equivale à função do limite. Como assim? Vejamos:
Agora só calculamos o limite e, no final, elevamos ao resultado que obtivermos!
Passo 5
Ainda temos, nesse caso, o problema de não poder aplicar L’Hôpital diretamente. A indeterminação não é passível pra aplicar a regra!
Dessa forma, podemos dividir o numerador e o denominador do conteúdo do logaritmo pra nos livrarmos da indeterminação que existe dentro dele. Assim, vamos ter:
Agora,a indeterminação que chegamos agora é , que nós podemos facilmente converter em trabalhando em cima de da seguinte forma:
Dessa forma, já podemos aplicar L’Hôpital e calcular o limite!
Passo 6
Derivando numerador e denominador (usando a regra da cadeia), vamos ter:
Aqui, continuamos com uma indeterminação. Só que agora do tipo . Nesse caso podemos aplicar de novo L’Hôpital, derivando numerador e denominador novamente. Vamos ter:
Dividindo numerador e denominador pelo termo de com maior grau do denominador, que é , temos:
Por fim, temos como resposta:
Então a equação da assíntota horizontal que temos é