Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.6 - Ex. 52

Faça uma conjectura sobre o limite traçando o gráfico da função envolvida com um recurso computacional; verifique sua conjuctura usando a regra de L’Hôpital.

lim x → π 2 - ⁡ 4 t g x 1 + sec ⁡ x

Passo 1

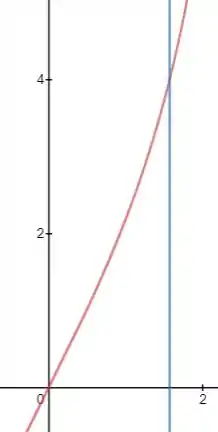
Quando montamos o gráfico dessa função computacionalmente (função em vermelho), podemos observar que quando temos x = π 2 (representado em azul) se aproximando pelo lado negativo, temos y   la na casa dos 4 aprximadamente. Vamos ver se é isso mesmo calculando o limite...

Passo 2

Se substituirmos t g   p o r s e n   x cos ⁡ x e substituirmos também sec ⁡ p o r 1 cos ⁡ x ficaremos com:

lim x → π 2 - ⁡ 4 t g x 1 + sec ⁡ x = lim x → π 2 - ⁡ 4   s e n   x cos ⁡ x 1 + 1 cos ⁡ x

lim x → π 2 - ⁡ 4   s e n   x cos ⁡ x + 1

4   s e n   π 2 cos ⁡ π 2 + 1 = 4 × 1 0 + 1 = 4

Resposta

4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar os seguintes limites com auxilio das regras de L’Hospital. lim x → + ∞ ⁡ 2 x - 1 2 x
Determinar os seguintes limites com auxilio das regras de L’Hospital. lim x → 0 + ⁡ ln ⁡ s e na x ln ⁡ s e nx
Determinar os seguintes limites com auxilio das regras de L’Hospital. lim x → + ∞ ⁡ x ln ⁡ x x + ln ⁡ x
Determinar os seguintes limites com auxilio das regras de L’Hospital. lim x → π 4 ⁡ 1 - t gx s e c 2 x
Determinar os seguintes limites com auxilio das regras de L’Hospital. lim x → 0 + ⁡ x s e n x