Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.6 - Ex. 49
Faça uma conjectura sobre o limite traçando o gráfico da função envolvida com um recurso computacional; verifique sua conjuctura usando a regra de L’Hôpital.
Passo 1
Quando montamos o gráfico dessa função computacionalmente, podemos observar que quanto maior o x, mais a função se aproxima do zero, mas sem tocá-la, o que nos faz acreditar que quando x vai para o infinito, temos 0 como resultado do limite.
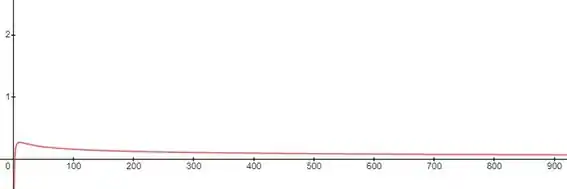
Passo 2
Aplicando a regra de l’hospital temos então:
Opa, então confirmamos que nosso limite realmente vai para zero!
Resposta
Exercícios de Livros Relacionados
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.Se n for escolhido suficientemte grande, então lim x → ∞ ln x n x = ∞
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.A regra de L’Hospital não é aplicável a lim x → - ∞ ln x x
Calcule o limite dado sem usar a regra de L’Hospital e depois use-a para conferir sua resposta. a lim x →0 s e n x t g x
Encontre o limite. lim x → ∞ + ln x x
Calcule o limite dado sem usar a regra de L’Hospital e depois use-a para conferir sua resposta. b lim x → ∞ 2 x - 5 3 x + 7