Faça a correspondência entre o campo vetorial e a figura rotulada de . Justifique suas escolhas.

Passo 1
Oi, galera! Tudo bem?
A questão nos dá 4 imagens de campos vetoriais e quer que a gente identifique qual delas descreve o campo:
Esse vetor tem componentes:
A componente aponta na direção e a componente na direção . Então para cada direção temos uma função, aqui é a função pra direção e a função para a direção . Então para cada quadrante vamos analisar o comportamento dos pontos para as funções e e assim conseguimos entender para qual direção cada componente do vetor deve estar apontando, e assim identificar nosso campo correto.
Bora!
Passo 2
Vamos fazer a análise de cada quadrante de cada vez:
- Primeiro quadrante, na região de e , as componentes dos vetores são positivas. Então as duas componentes do vetor devem estar apontando para a direção positiva, tanto do eixo quanto do eixo .
- Segundo quadrante: No segundo quadrante, os valores das funções são negativas para ( e positivas para .
- No terceiro quadrante: ambas as componentes são negativas, já que os valores de e também são negativos.
- No quarto quadrante: as componentes verticais são positivas e horizontais são negativas, já que é negativo e é positivo.
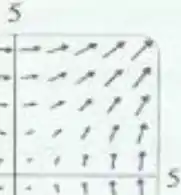
Então nesse quadrante os vetores devem ter componentes horizontais positivas e verticais negativas.

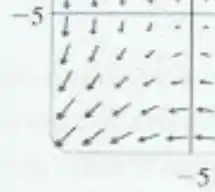
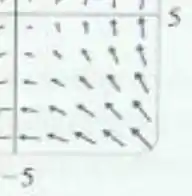
Então, campo vetorial pertence ao gráfico .
Além disso, quanto mais perto da origem, menores são os vetores, já que menores são os valores de e . Quanto mais longe, maiores.
Resposta
.