Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 12

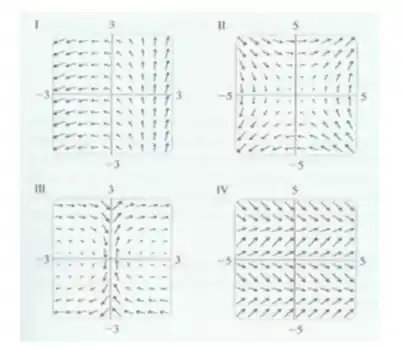
Faça a correspondência entre o campo vetorial F → e a figura rotulada de I - I V . Justifique suas escolhas.

F → x , y = 1 , s e n   y

Passo 1

Oiii, galera! Tudo bem?

A questão nos dá 4 imagens de campos vetoriais e quer que a gente identifique qual delas descreve o campo:

F → x , y = 1 , s e n   y

Esse vetor tem componentes:

F → x , y = 1   i + s e n   y   j

A componente i   aponta na direção x e a componente j na direção y . Então para cada direção temos uma função, aqui é a função 1 pra direção i e a função s e n   y para a direção j . Então para cada quadrante vamos analisar o comportamento dos pontos x e y   do plano para as funções 1 e s e n   y e assim conseguimos entender para qual direção cada componente do vetor deve estar apontando, e assim identificar nosso campo correto.

Vamos lá!

Passo 2

F → x , y = 1   i + s e n   y   j

  • Primeiro quadrante: x > 0 e y > 0

    • Nosso vetor tem comprimento 1 constante na direção horizontal. A função seno oscila entre valores positivos e negativos, então nossos vetores tem que estar mudando de direção verticalmente, apontando para baixo e para cima.

  • Segundo quadrante: x < 0 e y > 0

    • Nosso vetor tem comprimento 1 constante na direção horizontal. A função seno oscila entre valores positivos e negativos, então nossos vetores tem que estar mudando de direção verticalmente, apontando para baixo e para cima.

  • Terceiro quadrante: x < 0 e y < 0

    • Nosso vetor tem comprimento 1 constante na direção horizontal. A função seno oscila entre valores positivos e negativos, então nossos vetores tem que estar mudando de direção verticalmente, apontando para baixo e para cima.

  • Quarto quadrante: x > 0 e y < 0

Nosso vetor tem comprimento 1 constante na direção horizontal. A função seno oscila entre valores positivos e negativos, então nossos vetores tem que estar mudando de direção verticalmente, apontando para baixo e para cima.

O campo vetorial F → x , y = 1 , s e n ( y )     pertence ao gráfico I V pois olhando as componentes horizontais, elas são constantes e apontam para a direita.

Além disso, as componentes verticais parecem seguir um padrão, típico de funções periódicas como o seno. Como mostramos acima, todos os quadrantes seguem o mesmo padrão, então nosso campo é o I V .

Resposta

I V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12. Determinar o trabalho realizado pela força f → = y z e x z ,e x z , x y e x z + 1 para deslocar uma partícula ao longo da curva y=2/x do ponto A(-1,-2,0) ao ponto B(-2,-1,0). Esse trabalho é maior
9. Calcular ∫ C f → ⋅ d r → , onde f → = r → r → 3 , r → = x , y , z , ao longo dos seguintes caminhos:(d) intersecção das superfícies z = x 2 + y 2 , x=2, do ponto A(2,0,2) a B(2,4,2 5 )
9. Calcular ∫ C f → ⋅ d r → , onde f → = r → r → 3 , r → = x , y , z , ao longo dos seguintes caminhos:(a) elipse x 2 4 + y 2 = 4 , z=2, uma volta completa no sentido anti-horário
15. Calcular o trabalho realizado pela força f → = 2 x + z + 4 i → + y 2 - 3 z - 1 j → + ( x - 3 y + z ) k → sobre uma partícula, ao longo de C, de A(2,4,2) a B(2,0,0), onde C é:(b) a parábola y = z 2
9. Calcular ∫ C f → ⋅ d r → , onde f → = r → r → 3 , r → = x , y , z , ao longo dos seguintes caminhos:(b) quadrado x + y = 1 ,z = 0 , no sentido anti-horário;