Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 13
Faça a correspondência entre o campo vetorial e a figura rotulada de . Justifique suas escolhas.
Passo 1
E aí, pessoal! Tranquilo?
A questão nos dá 4 imagens de campos vetoriais e quer que a gente identifique qual delas descreve o campo:
Esse vetor tem componentes:
A componente aponta na direção e a componente na direção . Então para cada direção temos uma função, aqui é a função pra direção e a função para a direção . Então para cada quadrante vamos analisar o comportamento dos pontos e do plano para as funções e e assim conseguimos entender para qual direção cada componente do vetor deve estar apontando, e assim identificar nosso campo correto.
Vamos lá!
Passo 2
Olhando nosso vetor, vemos que tanto sua componente horizontal quanto sua componente vertical não dependem de em suas funções.
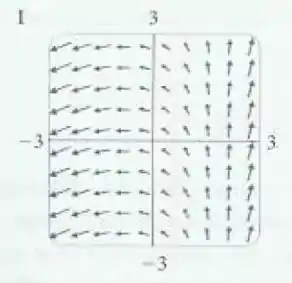
O campo vetorial pertence ao gráfico pois são independentes de . Notem que os vetores ao longo da mesma linha vertical (por exemplo, ) são iguais.
E, à medida que vamos indo mais para a direita, ambas componentes vão ficando maiores.