Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 15
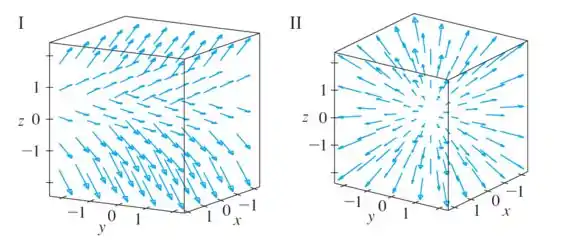
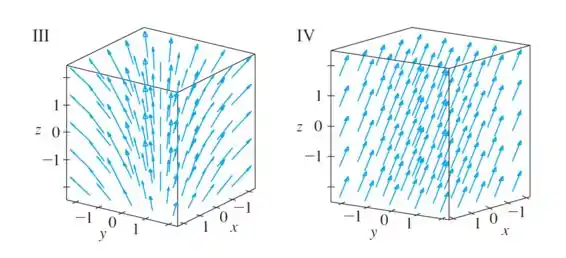
Faça a correspondência entre o campo vetorial em e a figura rotulada de . Justifique suas escolhas.
Passo 1
Oi galera, tudo bem?
Essa questão deu pra gente um campo vetorial e precisamos descobrir qual figura representa ele!
Pra isso, vamos olhar pra expressão de definição dele:
E entender como ela se comporta conforme mudamos o ponto .
Com isso, vemos qual das figuras bate com o que a gente analisar.
Passo 2
Esses na expressão representam as três coordenadas do vetor, então:
Ou seja, nosso campo é um campo constante!
Independente do ponto , o vetor resultante vai sempre ser .
A única figura que representa um campo que tem o mesmo vetor em todos os pontos (mesmo tamanho, e apontando pra mesma direção) é a .
Resposta
Exercícios de Livros Relacionados
2 ) Considere o campo vetorial F ( x ,y )=i +( x-y ) j . Desenhe F(x, y) nos pontos da reta b )y=x-1
2 ) Considere o campo vetorial F ( x ,y )=i +( x-y ) j . Desenhe F(x, y) nos pontos da reta c )y=x-2
3 ) Considere o campo vetorial g ( x ,y )=i +x y j . Desenhe g(x,y) nos pontos da hipérbole xy = 1, com x0
Calcule o trabalho realizado pelo campo de forças F x , y = ( x 2 - y 2 , 2 x y ) ao mover uma partícula ao longo da fronteira do quadrado limitado pelos eixos coordenados e pelas retas x = a e y = a
7. Determine uma função potencial para cada campo gradiente F dado b. F x , y = 2 x y 2 - y 3 ,2 x 2 y - 3 x y 2 + 2