Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.2 - Ex. 2-c
2 ) Considere o campo vetorial . Desenhe F(x, y) nos pontos da reta
Passo 1
O nosso campo vetorial tem o formato
Se estamos na reta
Entoa podemos substituir esses valores no nosso campo, assim ficamos com
Passo 2
Abaixo podemos ver esse campo geometricamente
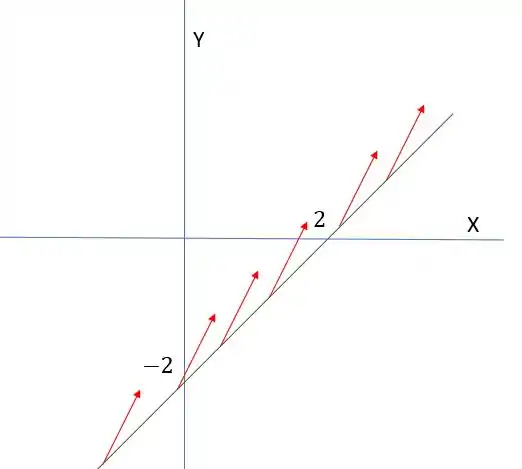
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Encontre a integral de linha de ƒ(x, y) = x – y + 3 ao longo dacurva r(t) = (cos t)i + (sen t)j, 0 ≤ t ≤ 2p.
Calcule ∫ C ( x y + y + z ) d s ao longo da curva r ( t ) = 2 t i + t j + ( 2 - 2 t ) k , 0 ≤ t ≤ 1
Calcule ∫ C ( x y + y + z ) d s ao longo da curva r ( t ) = 2 t i + t j + ( 2 - 2 t ) k , 0 ≤ t ≤ 1
Encontre a integral de reta de ƒ(x, y) = yex² ao longo da curvar(t) = 4ti – 3tj, –1 ≤ t ≤ 2.
Trabalho Encontre o trabalho realizado pelo gradiente deƒ(x, y) = (x + y)2 no sentido anti-horário em torno da circunferência x2 + y2 = 4 de (2, 0) a si próprio.