Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.3 - Ex. 5
Calcule o trabalho realizado pelo campo de forças ao mover uma partícula ao longo da fronteira do quadrado limitado pelos eixos coordenados e pelas retas e ( no sentido anti-horário.
Passo 1
Falaaaa, vamo lá resolver esse problema ai?!
Beleza, temos o nosso campo . A nossa partícula se moveu ao longo da fronteira de um quadrado, da só uma olhada:
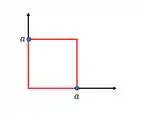
Vamos fazer algo semelhante ao que mostra no exemplo 6.5, vamos “quebrar” esse quadrado em 4 curvas, olha só:
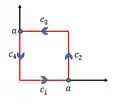
Daí, teremos que o trabalho realizado pelo campo ao mover a partícula será dado por:
Passo 2
Beleza, já sabemos o caminho a se seguir. Vamos agora parametrizar essas curvas, para podermos fazer a integral de linha. Assim, teremos:
Cara, a nossa primeira curva tem variação apenas em , no eixo ela tem componente igual a zero. Na segunda curva, temos que ela está fixa em , mas varia em . Na terceira curva, temos a variação em em direção a , mas fixa em . Já a nossa quarta curva, temos fixo e a variação em em direção a .
Temos as parametrizações e as derivadas delas, mas para que isso?! Lembra da nossa denotação da integral de linha:
Passo 3
Agora, vamos lá substituir cada curva em sua respectiva integral: