Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 24
Faça uma correspondência entre as equações paramétricas e os gráficos (identificados com números de ). Justifique sua escolha.
Passo 1
Galerinha, olha o que acontece se manipularmos um pouco as equações:
Ou seja, temos que a curva está contida no cilindro circular com geratriz paralela ao eixo :
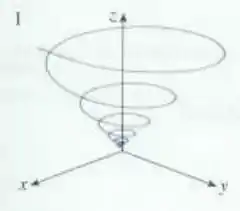
Apenas com essas informações, poderíamos ficar em dúvida entre o gráfico e o gráfico . Porém, sabendo que , teremos que quando , e o único gráfico que mostra em algum momento é:
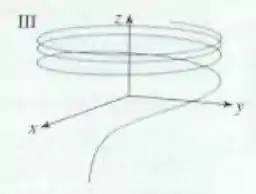
Resposta
Gráfico
Exercícios de Livros Relacionados
Combine as equações paramétricas com os gráficos (rótulo I-VI). Dê razões para suas escolhas: x = cos 8 t , y = sin 8 t , z = e 0,8 t , t ≥ 0
Esboce a curva com a equação vetorial fornecida. Indique uma seta, a sentido na qual t aumenta: r t =t 2 - 1 , t
Combine as equações paramétricas com os gráficos (rótulo I-VI). Dê razões para suas escolhas: x = t , y = 1 ( 1 + t 2 ) , z = t 2
Combine as equações paramétricas com os gráficos (rótulo I-VI). Dê razões para suas escolhas: x = t cos t , y = t , z = t sin t , t ≥ 0
Combine as equações paramétricas com os gráficos (rótulo I-VI). Dê razões para suas escolhas: x = cos t , y = sin t , z = cos 2 t