Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 12.6 - Ex. 26
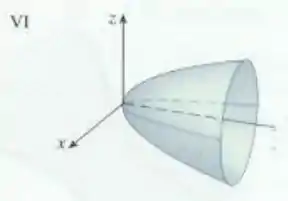
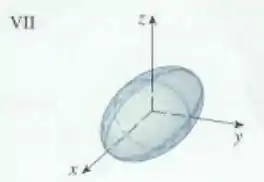
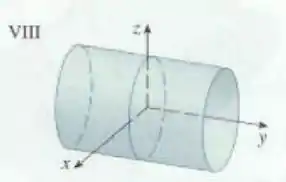
Faça uma correspondente entre a equação e seu gráfico (identificado por -). Justifique sua escolha.
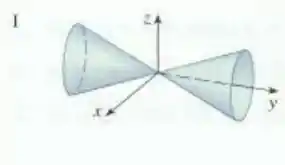
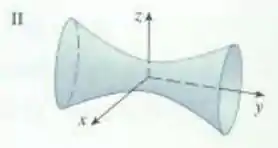
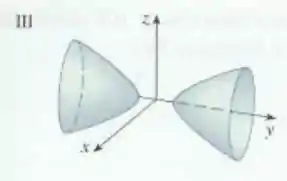
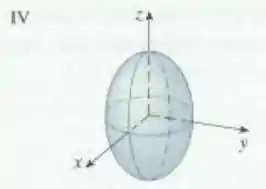
Passo 1
Galera, primeiro vamos fazer umas modificações na nossa equação pra ela ficar parecida com uma que já conhecemos, ok?
Passo 2
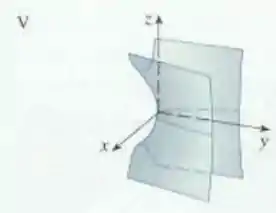
Show! Agora veja como a equação a que chegamos se parece com a equação do paraboloide hiperbólico:
A diferença entre as duas é que o termo elevado à primeira potência passa a ser na nossa equação, então ela realmente representa um paraboloide hiperbólico, sendo a nossa única opção:
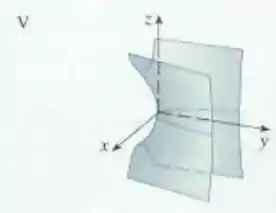
Resposta
Gráfico
Exercícios de Livros Relacionados
Coloque a equação na forma-padrão, classifique a superfície e esboce-a. 4 x 2 + y 2 + 4 z 2 - 4 y - 24 z + 36 = 0
Use um computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela retangular até conseguir uma boa visão da superfície. x 2 -
Esboce a região delimitada pelas superfícies z = x 2 + y 2 e x 2 + y 2 = 1 para 1 ≤ z ≤ 2 .
Use um computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela retangular até conseguir uma boa visão da superfície. x 2 -
Use um computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela retangular até conseguir uma boa visão da superfície. - 4 x