Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.3 - Ex. 21
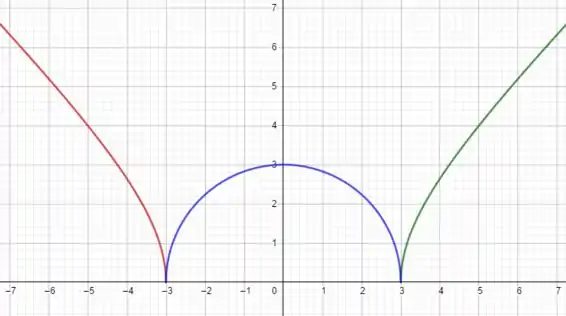
Faça um esboço do gráfico e ache o limite indicado, se existir; se não existir, indique a razão disso.
Passo 1
Faala ae, beleza?
Vamos começar fazendo um esboço de . Para isso temos que entender um pouquinho só como é essa nossa .
O enunciado disse que:
Beleza! Então, teremos uma hipérbole para e . E teremos uma semicircunferência de raio em . Ok? Plotando esse cara, chegamos nesse gráfico:
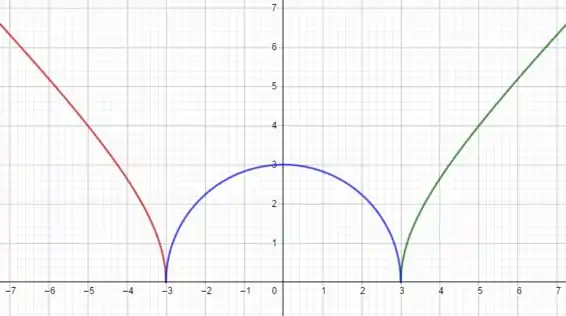
Deixei cada parte da função colorida para entender melhor os intervalos, beleza? Então, em vermelho e verde, temos as hipérboles. E em azul, a semicircunferência. Agora, vamos calcular esses limites!
Passo 2
Letra
Agora vamos aos limites que ele pediu
Aqui, temos que ver o comportamento da função quando se aproxima de pela esquerda. Que é se aproximar de por valores menores que .
Olhando o gráfico, chegando perto de pela esquerda, a nossa função se aproxima de .
Podemos achar isso calculando o limite, também! Quando temos valores menores que , nossa função se comporta de acordo com , certo? Só olhar para a definição:
Então, para calcular esse limite com valores pela esquerda de :
Substituindo :
Opa, exatamente o que esperávamos!
Passo 3
Letra
Agora o outro
Aqui, temos que ver o comportamento da função quando se aproxima de pela direita. Que é se aproximar de por valores maiores que .
Olhando o gráfico, chegando perto de pela direita, a nossa função se aproxima de , também.
Da mesma forma que no passo anterior, podemos achar isso calculando o limite, também! Quando temos valores maiores que , nossa função se comporta de acordo com , certo? Só olhar para a definição:
Então, para calcular esse limite com valores pela direita de :
Substituindo :
Bateu mais uma vez!
Passo 4
Letra
Para o limite que ele pediu, temos que comparar os limites laterais.
Se eles forem iguais, o limite em vai existir e será esse valor. Se eles forem diferentes o limite não existe.
Pelas letras e , os dois limites laterais vão ser , são iguais. Logo, se os limites laterais:
Nós temos que:
Passo 5
Letra
Agora vamos aos limites que ele pediu
Aqui, temos que ver o comportamento da função quando se aproxima de pela esquerda. Que é se aproximar de por valores menores que .
Olhando o gráfico, chegando perto de pela esquerda, a nossa função se aproxima de .
Podemos achar isso calculando o limite! Quando temos valores menores que , nossa função se comporta de acordo com , certo? Só olhar para a definição:
Então, para calcular esse limite com valores pela esquerda de :
Substituindo :
Passo 6
Letra
Agora o outro
Aqui, temos que ver o comportamento da função quando se aproxima de pela direita. Que é se aproximar de por valores maiores que .
Olhando o gráfico, chegando perto de pela direita, a nossa função se aproxima de .
Podemos achar isso calculando o limite! Quando temos valores maiores que , nossa função se comporta de acordo com , certo? Só olhar para a definição:
Então, para calcular esse limite com valores pela direita de :
Substituindo :
Passo 7
Letra
Para o limite que ele pediu, temos que comparar os limites laterais.
Se eles forem iguais, o limite em vai existir e será esse valor. Se eles forem diferentes o limite não existe.
Pelas letras e , os dois limites laterais vão ser , são iguais. Logo, se os limites laterais:
Nós temos que:
Resposta
