Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.4 - Ex. 14
Faça um esboço do gráfico de cada função. Não use a calculadora. Use somente os gráficos dados nas Figuras 3 e 13 e, se necessário, as transformações da Seção 1.3 .
Passo 1
Fala aí, pessoal. Tudo certinho com vocês?
Bom, essa questão pede para que a gente use os gráficos da figura 3 e da figura 13 do livro, Fazendo as transformações que forem necessárias, para esboçar o gráfico da função
Então precisaremos entender que gráficos são esses, como eles se parecem com a nossa função, e quais transformações devemos fazer para obter o gráfico que queremos.
Vem que te mostro como vamos fazer tudo isso.
Passo 2
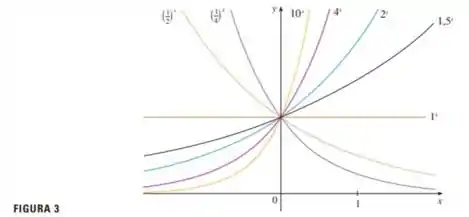
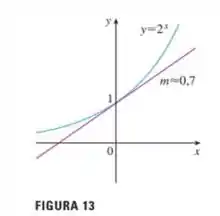
Primeiro vamos ver qual é a figura 3 e a figura 13. Do livro, temos:
E
Bom pessoal, como nossa função é
Podemos reescrevê-la como
O gráfico mais próximo é o que está em cinza na figura 3. Nela podemos ver como o gráfico da função pode ser esboçado, pois ela é a função
Repare em algumas características importantes. Essa função corta o eixo em , e se aproxima do eixo , mas não o atravessa, quando os valores de tendem para .
Porém, a função no nosso exercício não é exatamente igual a esta. Temos está função subtraída de unidades. Isso indica que precisamos de uma transformação.
Passo 3
Na seção 1.3, aprendemos que quando temos uma função do tipo devemos fazer um deslocamento vertical do gráfico da função para baixo. No nosso caso, duas unidade para baixo. Com isso, nossa função se tornará:
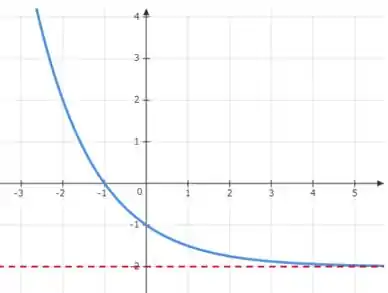
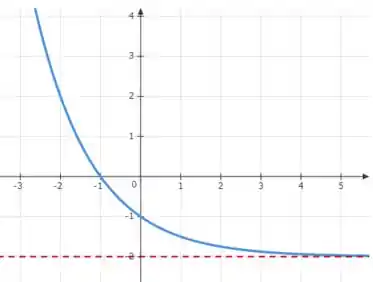
Que tem corta o eixo em , duas unidades a menos que nossa função base, e se aproxima da reta , mas não a atravessa, quando os valores de tendem para . Mostrando com clareza o deslocamento da curva.
Resposta
