Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.2 - Ex. 28
A tabela mostra as distâncias dos planetas ao Sol (tomando como unidade de medida a distância da Terra ao Sol) e seus períodos (tempo de resolução em anos).
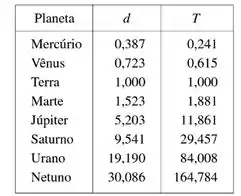
- Ajuste um modelo de função potência aos dados.
- A terceira Lei de Moimento Planetário de Kepler diz que “O quadrado do período de revolução de um plante é proporcional ao cubo de sua distância ao Sol”. Seu modelo confirma a lei de Kepler?
Passo 1
Eaee!!! Belezinha? Bom... a questão quer que ajustemos um modelo de função potência para os seguintes dados:
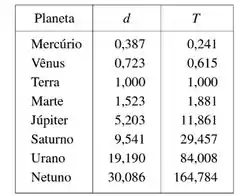
Onde é a distância dos planetas ao Sol (em relação a distância da Terra ao Sol) e são seus respectivos períodos (em anos).
Para isso, sabemos que o modelo de função de potência é dado por:
Onde e são parâmetros do ajuste.
Dessa forma, com o auxílio de um software matemático (pode ser o excel, por exemplo), devemos aplicar os pontos e analisar a curva resultante para assim podermos determinar os valores dos parâmetros informados.
😉
Passo 2
Então... fazendo o eixo das ordenadas e , o das abscissas, temos os pontos e a seguinte curva resultante:
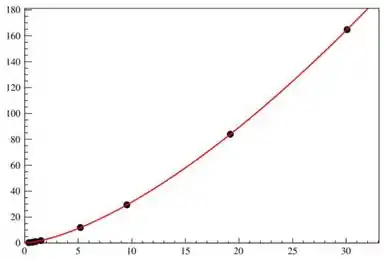
Assim, vemos que os parâmetros encontrados são:
O que faz total sentido, visto que, pela Terceira Lei de Kepler, temos:
Veja que o expoente ficou bem próximo do valor encontrado!!
Assim, podemos concluir que modelo confirma a lei de Kepler.
Entendeu direitinho? Responde aee ;)
Resposta
O modelo confirma a lei de Kepler.