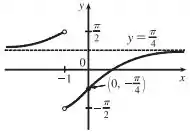
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Fala aí, eu sou o Rafha do Responde Aí e vou te ajudar em mais uma questão!Bora lá
Aqui temos que fazer o gráficoda seguinte função:
E aqui vamos seguir o seguinte roteiro para esboçar o gráfico dela.
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Verificar se há simetria par, isso é:
Verificar se há simetria ímpar, isso é:
E verificar se há periodicidade:
D. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
E. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
F. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
G. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
H. Esboçar a função juntando as informações obtidas.
Passo 2
Nossa função é:
A gente precisa lembrar certinho dos passos, em? Se seguir tudo bonitinho todo mundo acha a curva!!
Primeiro a gente procura o domínio da função. Olhando pra ela, vemos que a base da fração não pode ser zero, precisa ser diferente de , então,
Agora procuramos intersecções.
Há intersecção com o eixo se for possível encontrar
Um arco cuja tangente é igual há é o arco
O intercepto de é .
O intercepto de é quando fazemos , logo temos:
O arco cuja tangente vale zero é , logo:
Portanto,
O Intercepto de é , já que fazendo encontramos esse valor.
Testando as três possibilidades de simetria:
E não temos um período onde essa função se repita.
Já que nenhuma das três possibilidades acontece, não há simetria.
Agora tem que lembrar lá do começo como resolve limite, porque vamos procurar as assíntotas.
Então bora lá.
Temos que
Temos que resolver essa indeterminação, para isso, colocamos o de maior potência do numerador e do denominador em evidência:
Podemos agora cortar e sabemos que quando vai para infinito resulta em , logo:
Então é uma assíntota horizontal. E ela ocorre tanto quando vai para mais infinito quanto vai para menos infinito.
Para procurar por assíntotas verticais, vamos olhar no ponto de descontinuidade, isso é, em .
Quando tende a mais infinito, a função tende para e quando tende a menos infinito, tende para .
Dessa forma, avaliando os limites laterais:
E pelo outro lado temos:
Portanto, não temos assíntota vertical nesses pontos, mas sabemos como a função se comporta nessa descontinuidade:
Passo 3
A gente vai entrar agora na parte das derivadas, não pode esquecer em!
Primeiro vamos encontrar os intervalos em que a função cresce ou decresce calculando a derivada primeira:
A derivada do arcotangente é:
Usando essa derivada e a regra da cadeia, teremos:
Usando a regra do quociente, temos:
Realizando essa multiplicação, teremos:
Como todos os termos dessa conta são positivos, temos que:
Em todo o domínio.
Então, está crescendo em e
Agora é a hora de achar os pontos extremos.
No caso dessa função, ela apenas cresce, então não existem pontos máximos ou mínimos.
Passo 4
O último passo antes de montar o gráfico é achar as concavidades e pontos de inflexão, que vamos encontrar calculando a segunda derivada:
Derivando temos:
Avaliando o sinal dessa segunda derivada, temos que o denominador será sempre positivo.
Portanto, quando for positivo, a segunda derivada é negativa, pois está multiplicada por um fator .
Sendo assim a função é côncava para baixo quando .
Analogamente ela é côncava para cima quando .
E é um ponto de inflexão.
Passo 5
Esboçando o gráfico, com as informações obtidas, temos:
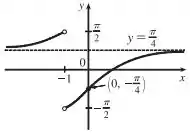
Resposta