Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.3 - Ex. 19
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção e então aplicando as transformações apropriadas.
Passo 1
Eaee, belezinha??? Bom... a questão nos fala para fazer o gráfico da seguinte função:
Mas para isso, devemos utilizar as funções básicas dadas na seção .
Assim, vamos comparando com essas funções e assim vamos construindo o gráfico, certinho??
Se liga... Como temos um aparecendo ali na função, uma das funções parecidas é:
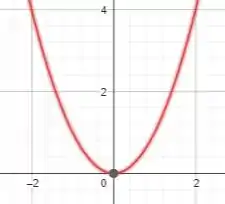
Então vamos analisar qual a diferença entre as duas funções para poder definir como será o gráfico, beleza?
Então bora lá!! 😉
Passo 2
Vamos primeiro analisar o que acontece com a função certo?
Quais mudanças ela vai causar na função inicial que tomamos.
Olhando para a função
Perceba que podemos completar quadrados, e enquadrar melhor nas possibilidades que o livro nos dá do que acontece com a função, certo?
Essa função pode ser reescrita como:
Agora ficou mais fácil de comparar com , né?
Passo 3
Perceba que, como , então podemos expressar como:
Concorda?
O sinal de menos, na frente da função , nos fornece uma reflexão do gráfico de , com relação ao eixo , E o , do dentro da função, um deslocamento de uma unidade para a esquerda. Já o que aparece antes do , um deslocamento de uma unidade para cima.
Então fechou! Vamos desenhar , ok?
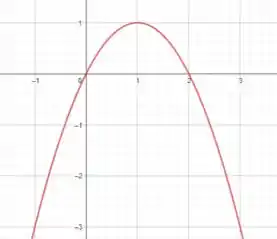
Mas calma que ainda não acabamos.
Olhamos em comparação à pois era essa função disponível.
Nossa questão pede
Então agora vamos comparar essa função com que é mais parecida com o que a gente precisa.
Passo 4
Estamos acabando! Forçaaa!
Se a gente considerar é so perceber que Corresponde a:
Que pelo livro, é o mesmo que deslocar o gráfico de em 1 unidade para cima e deslocar duas casas para esquerda por conta do sinal negativo em :
Então agora é só desenhar, beleza?
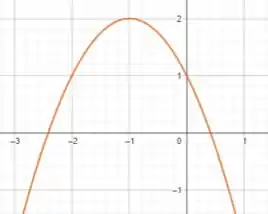
Resposta
