Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.3 - Ex. 17
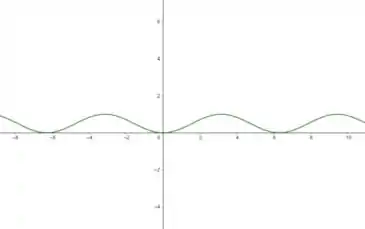
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção e então aplicando as transformações apropriadas.
Passo 1
Eaee, belezinha?? Bom... queremos plotar o gráfico da seguinte função:
Para isso, o enunciado quer que a gente faça esse gráfico a partir de uma das funções básicas dadas na seção e apliquemos as transformações apropriadas.
Nesse caso, iremos verificar a função dessa seção que mais se assemelha com a nossa.
Com isso, iremos verificar o que significam as diferenças entre as duas na plotagem.
Agora bora lá!! 😉
Passo 2
Antes de começar vamos dividir a nossa função para analisar ela em partes.
Vamos fazer . Assim, temos:
Assim iremos comparar primeiro e rapidamente conseguimos extrair a informação sobre certo?
Para isso, vamos considerar .
Perceba que corresponde a
Ou seja, multiplicamos por e depois somamos
Fazer isso, segundo o livro, significa que devemos refletir o gráfico de em relação ao eixo e em seguida, deslocar unidade para cima.
Nesse sentido, temos que o gráfico de é dado da seguinte forma:
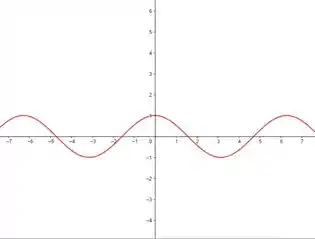
Perceba que é uma cossenoide!!
Assim, fazendo as alterações que acabamos de mencionar, temos:
Acabou? Não. Ainda não chegamos onde precisamos. Mas falta bem pouco hihi
Passo 3
A função que queremos desenhar o gráfico é , mas vimos anteriormente que Acabamos de desenhar o gráfico de
Então agora é só comprimir verticalmente o gráfico de por um fator de :
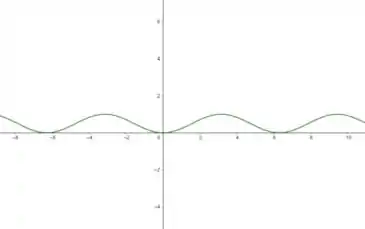
Entendeu direitinho?? Responde aee 😉
Resposta
