Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.3 - Ex. 17
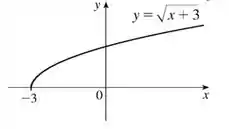
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção e então aplicando as transformações apropriadas.
Passo 1
Fala galerinha!
A questão aqui quer que a gente use umas funções de referência do livro e faça transformações pra chegar no gráfico da nossa função:
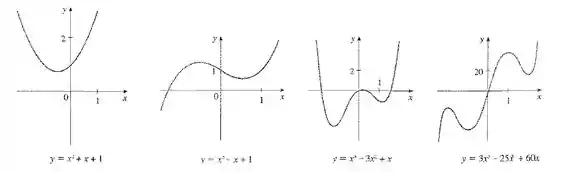
Mas que funções são essas da seção 1.2? Bom, são muitas! Tem funções polinomiais...
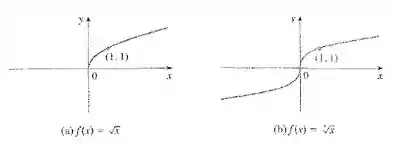
... funções raiz...
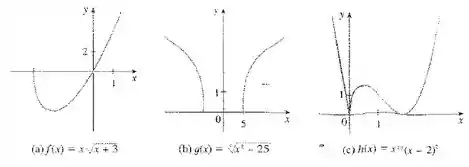
... funções algébricas de vários tipos...
... trigonométricas, exponenciais e logarítmicas...
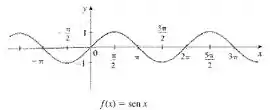
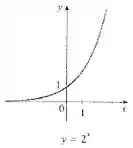
Mas no meio desse tanto de função, qual será a que a gente pode usar???
Bom, a nossa estratégia é comprar as funções. Qual é mais parecida? O que elas tem em comum e o que tem de diferente?
Se você reparar bem na função que nos temos, ela é uma raiz de e ela é bem parecidinha com a função , só muda esse +3 ali dentro.
Então vamos partir da e fazer as transformações necessárias.
Passo 2
Temos muitas formas de transformar as funções, podemos somar ou subtrair valores no , podemos multiplicar por constantes e etc... E cada operação vai dar um efeito no gráfico.
No geral, multiplicar por constantes dá efeitos de contração ou de esticar o gráfico em alguma direção. E somar a subtrações costumam gerar deslocamentos lineares.
Então vamos partir do gráfico que o livro nos dá pra :
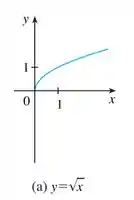
Nesse caso, nós temos um termo junto com o . Isso quer dizer que pra obter o mesmo resultado temos que colocar uma entrada subtraída de 3. Em outras palavras, se substituirmos na nossa refrência, temos o mesmo resultado que se substituirmos na nossa função aqui da questão.
Visualmente falando, quando somamos ou subtraímos um valor que ta juntinho dá variável independente, nós estamos deslocando a função no eixo horizontal, sacou? E nesse caso, somar vai deslocar o gráfico unidades para esquerda, ficando assim:
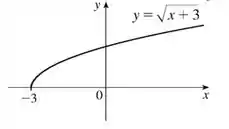
Pronto! Essa já é a nossa resposta ;)
Resposta
O gráfico de é:
