Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 75
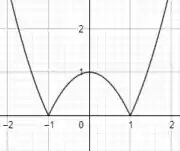
Faça o gráfico da função:
Passo 1
Para resolvermos essa questão vamos começar fazendo uma análise lógica do problema, tudo bem?
Se substituirmos quaisquer valores de na função, o valor de sempre será positivo devido ao módulo. Sendo assim, para plotarmos esse gráfico, vamos descobrir qual é o gráfico da função interna, que é , beleza? Achando as raízes da função, temos:
Sendo assim, sabemos que a parábola vai interceptar o eixo em 1 e -1! Plotando isso, teremos:
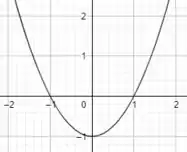
Passo 2
Perceba que no gráfico, para valores de entre [-1,1] a função dá um valor negativo, não é mesmo? Como a função é modular, isto é, só admite valores positivos, então o que devemos fazer é espelhar essa parte negativa em torno do eixo . Se liga como ficará o gráfico!
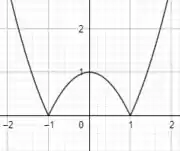
Resposta
O gráfico de é:
Exercícios de Livros Relacionados
a) Como estão relacionados o gráfico de y = f ( | x | ) e o gráfico de f ?b) Esboce o gráfico de y = s e n | x | .c) Esboce o gráfico de y = | x | .
Começando com o gráfico de y = e x , escreva as equações correspondentes aos gráficos que resultam ao:(a) deslocar 2 unidades para baixo; (b) deslocar 2 unidades para a direita;(c) refletir em torno d
Começando com o gráfico de y = e x , encontre as equações dos gráficos que resultam ao (a) refletir em torno da reta y = 4 (b) refletir em torno da reta x = 2 .
Encontre o domínio da função:(a) f (x) = (1)/(1 + e^x) (b) f (x) = (1)/(1 - e^x)
Se f x = 5 x , mostre que f x + h - f ( x ) h = 5 x 5 h - 1 h