Faça um gráfico completo de indique os limites quando e localize todos os extremos relativos, os pontos de inflexão e as assíntotas (quando apropriado).
Passo 1
Vamos começar calculando os limites:
Vamos pensar um pouco. Como está elevado ao quadrado na função, esses limites serão iguais. E já que se:
Calcular esses limites, seria o mesmo que calcular esse limite:
Podemos fazer duas substituições e tentar calcular esse limite por dois caminhos. A primeira é fazer a substituição:
Sendo um número inteiro, nosso limite fica:
Mas se a gente usar a substituição:
A gente vê que usando caminhos diferentes, esse limite dá valores diferentes, isso significa que ele não existe. Então vamos dizer que:
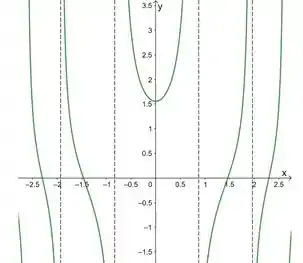
E vemos também que não temos assíntotas horizontais.
Passo 2
Para localizar os extremos relativos, precisamos calcular os valores de quando
Vemos que ele só zera em . Vamos fazer o teste da derivada segunda para classificar esse ponto. Vamos derivar com cuidado usando as regras do produto e da cadeia:
Como o valor da segunda derivada no ponto foi positivo, a gente tem que esse é um ponto de mínimo local.
Passo 3
Os pontos de inflexão ficam onde :
E como essa equação é muito complicada para resolver a mão, a gente deixa indicado que nossa função vai mudar de concavidade nos valores de que satisfazem essa equação.
Passo 4
Vamos verificar os pontos de descontinuidade de para descobrir se existem assíntotas verticais:
Sabemos que a função tangente é descontínua onde seu argumento é igual a . Sendo um número inteiro positivo. Igualando isso ao nosso argumento:
Descobrimos os pontos de descontinuidade. Vamos ver se temos assíntotas neles:
Temos então assíntotas verticais nesses pontos:
Passo 5
Agora é fazer o gráfico com tudo isso que a gente achou:
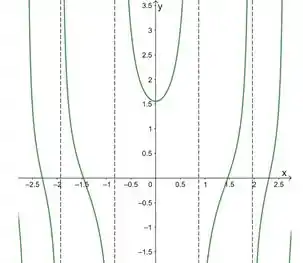
Resposta
ponto de mínimo
Pontos de inflexão quando
Assíntotas verticais em