Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 18
Um cartão retangular deve conter centímetros quadrados de área impressa. As margens no topo, na base e de um dos lados do cartão devem medir e a margem do outro lado deve medir . Quais devem ser as dimensões de um cartão desses que tenha a menor área?
Passo 1
Vamos refletir, a gente tem um cartão com margens. Sabemos que área dentro dessas margens tem que ser . Mas queremos descobrir as dimensões totais que minimizam a área.
Vamos desenhar:
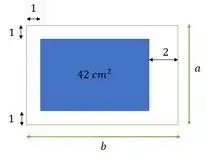
Para descobrir esses valores e , a gente precisa encontrar uma função que descreve essa área e descobrir o menor valor dela.
Vamos tentar fazer isso!
Passo 2
Vamos chamar cada lado do retângulo menor, a área impressa, de um nome. Um de e outro de :
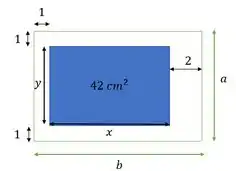
Fazendo isso, a gente pode escrever uma expressão para a área impressa:
Mas a gente sabe quanto ela tem que valer:
Passo 3
A gente também pode escrever uma expressão para e , olhando nossa figura:
Já que :
Agora olhando para :
Com isso, a gente pode escrever aquela tão sonhada expressão para a área total do cartão:
Passo 4
Com a expressão da área, podemos tentar descobrir o valor mínimo dela. Vamos verificar os valores de onde .
Vamos derivar essa função da área e igualar a zero:
Fazendo o MMC:
Igualando a zero:
Mas como é uma dimensão do retângulo menor, ele só pode ser um valor positivo. Então:
Já que só temos esse canditado, podemos dizer que a área vai ser mínima nele.
Passo 5
Para descobrir as dimensões é substituir o em e :
Ih, olha lá! Arrasamos!