Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.7 - Ex. 38
- Use um recurso gráfico computacional para gerar o gráfico de
e use-o para explicar o que acontece se aplicamos o Método de Newton com o valor inicial de . Verifique sua conclusão computando
- Use o gráfico gerado em (a) para explicar o que acontece se aplicarmos o Método de Newton com um valor inicial de Verifique sua conclusão computando
e use-o para explicar o que acontece se aplicamos o Método de Newton com o valor inicial de . Verifique sua conclusão computando
Passo 1
Fala aí!! Tudo joia?
Vamos começar do jeitinho que a questão pediu, gerando o gráfico. Você pode fazer isso no Geogebra, no Desmos...
Olha aqui:
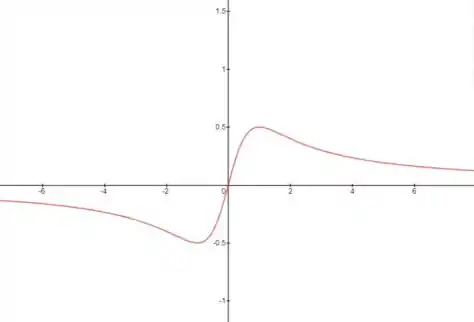
A gente tem um ponto de máximo ali próximo de e um mínimo em , então se a gente usar não vai dar muito certo essa aproximação não... vamos ver:
Passo 2
Para usar o método de Newton, a gente faz:
A nossa derivada aqui é:
Vamos aplicar no método agora:
Ou seja, com os números vão aumentando muito rápido a cada aproximação.
Passo 3
- Vamos ver agora com .
Ou seja, quando usamos os valores vão diminuindo de forma muito significativa.
Resposta
Em encontramos valores cada vez maiores e em encontramos valores cada vez menores.
Exercícios de Livros Relacionados
(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf
Esboce o gráfico de uma função que satisfaça todas as condições dadas.
f x = 1 2 x 4 - 4 x 2 + 3 (a) Encontre os intervalos crescentes e decrescentes.(b) Encontre os valores do máximo e mínimo.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use a in
Use os guias desta seção para traçar a curva. y = x - 1 2 x 2 + 1
Use os guias desta seção para traçar a curva. y = ln 1 + x 3